Линейные отображения и операторы

Линейные отображения.

Пусть и --- векторные пространства над .

Опр. Функция называется линейным отображением, если

.

Ядро: --- подпространство в .

Образ: --- подпространство в .

Опр. - множество всех линейных отображений .

Если мы знаем значение отображения на базисе, мы можем найти значение отображения на любом элементе по линейности.

Задание линейных отображений матрицами.

--- базис , --- базис . . Тогда .

Опр. --- матрица отображения в базисах , .

Пусть (т.к. разложение по базису в пространстве определено однозначно) или (столбцы).

Теорема. При фиксированных базисах в и существует взаимо однозначное соответствие между линейными отображениями из этого множества и матрицами х .

Введём обозначение матрицы}, .

1) Сюръективность : если взять матрицу , то для неё можно подобрать соответствующее линейное отображение: . Зададим на базисе : .

2) Инъективность. Пусть и . Тогда матрица разности отображений

Опр. Если и конечномерны, то ранг это размерность образа, .

Теорема.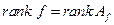

Пусть --- базис . Тогда Столбцы матрицы линейного отображения линейно независимы, это означает, что линейно независимы в .

Теорема.

Опять же фиксируем базис: пусть --- базис , --- базис , --- матрица в этих базисах. . Через обозначим . Тогда

(а) - решение системы линейных уравнений .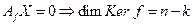

(б) (предыдущая теорема) = . Следовательно,

Следствие 1. Следующие условия, наложенные на , эквивалентны:

1) инъективно, 2) , 3) .

Следствие 2. Пусть , . Тогда .

1)Если , то . ().

2)Пусть теперь ядро = 0. . Тогда инъективно (по предыдущему следствию 1) и образ = , следовательно - образ отображения .

Замечание. Линейность Тогда линейна.

14.02.05

Линейные операторы.

Пусть V=W. Тогда – множество линейных операторов на V

(т.е. линейных отображений )

Если и линейные операторы на V, – скаляр, то

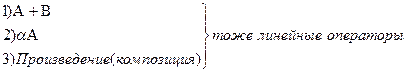
То есть – алгебра линейных операторов.

Линейная алгебра

(а) - векторное пространство над

(б) - векторное кольцо (относительно сложения и умножения)

(в)

Другое обозначение: =

Алгебра изоморфна алгебре матриц , где .

Дата добавления: 2015-10-26