Лаговые операторы

Альтернативным и более общим подходом к решению модели является использование лаговых операторов. По определению, лаговый оператор ставит в соответствие любой переменной ее же собственное значение, взятое с лагом: .

Чтобы увидеть все положительные стороны работы с лаговыми операторами, рассмотрим нашу модель без предположения, что следует процессу случайного блуждания. Мы можем отталкиваться от уравнения (6.60). Если предпринять те же самые действия, что и в случае вывода уравнения (6.62), но не предполагать при этом, что , то мы получим следующее уравнение:

, (6.75)

где константа - та же, что и прежде. Действительно, (6.75) принимает простой вид (6.62), если .

На первом этапе нужно переписать данное выражение в лаговых операторах. Величина может быть связана с с помощью лагового оператора: . Воспользуемся правилом, согласно которому в случае, когда применяется к выражению, содержащему ожидания, то происходит лаговый сдвиг самой переменной, но не периода, в котором формируются ожидания. Мы можем представить в виде .[14] Используя обозначение для обратной функции, мы можем записать . Аналогично, . С учетом этого, можно переписать (6.75) в виде:

, (6.76)

или

. (6.77)

Здесь обозначает оператор тождественного преобразования (т.е. для любого ). Так что представляет сокращенную форму записи для выражения , а - сокращенную форму записи для .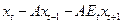

Заметим, что может быть «разложено» на , где как и раньше определяется выражением (6.70). Таким образом, мы получаем следующее уравнение:

. (6.78)

Данная форма записи, содержащая лаговый оператор, может быть проинтерпретирована естественным образом: выражение является сокращенной формой записи для за вычетом произведения на обратный лаговый оператор, примененный к . Т.е., данное выражение равно . С учетом определения , несложно показать, что (6.78) и (6.77) являются эквивалентными формами записи.

Так же как и в первом методе, чтобы найти решение, нам нужно избавиться от члена, содержащего ожидания относительно будущего значения эндогенной переменной. неявным образом присутствует в левой стороне (6.78), что определяется оператором . «Поделим» правую и левую сторону на . Это даст тот же результат, что и применение оператора . Действительно, произведение операторов и дает тождественный оператор . Таким образом, в левой части останется . В правой части будет стоять произведение операторов и , что даст следующий оператор: .[15] В итоге, выражение (6.78) переписывается в виде:

. (6.79)

Или без лаговых операторов:

. (6.80)

Уравнение (6.80) характеризует динамику устанавливаемых цен в зависимости от экзогенного процесса, определяемого предложением денег. Для того, чтобы описать динамику агрегированного уровня цен и выпуска, требуется просто подставить полученное выражение в формулы, определяющие 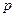и (т.е. и ).

В частном случае, когда следует процессу случайного блуждания, все ожидаемые величины будут равны , так что (6.80) принимает простой вид:

. (6.81)

Несложно показать, что выражение (6.68), с учетом того, что 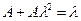, сводится к уравнению (6.65), . Таким образом, если следует процессу случайного блуждания, мы получаем тот же результат, что и выше. Но при этом мы также нашли решение модели для общего процесса .

Хотя использование лаговых операторов может показаться довольно замысловатой процедурой, это не более чем компактный способ проведения соверешенно обычных действий. Можно было бы вначале, путем нехитрых алгебраических преобразований, вывести (6.77), в виде, не содержащем лаговых операторов. Затем, с учетом того, что (6.77) должно соблюдаться для любого периода времени, можно записать

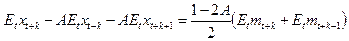(6.82)

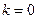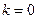для любого .[16] Уравнение (6.82) можно использовать следующим образом: если к левой части для прибавить левую часть для , умноженную на , затем прибавить левую часть для , умноженную на , и т.д., то это должно быть равно выражению в правой части для плюс выражение в правой части для , умноженное на , плюс выражение в правой части для , умноженное на , и т.д. В итоге это даст (6.80). Так что использование лаговых операторов вовсе не является обязательным – это просто упрощает запись и направляет ход решения.[17]

Дата добавления: 2015-10-30