Решение модели

Т.к. в каждом периоде половина цен на товары – это цены, установленные в предшествующем периоде, а другая половина цен – это цены, установленные два периода назад, агрегированный уровень цен будет равен

, (6.48)

где 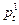- это цена, установленная для периода индивидом, который делал это в периоде , а - это цена, установленная для периода индивидом, который делал это в периоде . Коль скоро мы предположили, что процесс ценообразования основан на принципе эквивалентности детерминированному случаю, и все производители в данном периоде решают одну и ту же задачу, цена 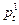будет равна ожидаемой в периоде оптимальной цене , а цена будет равна ожидаемой в периоде оптимальной цене . Таким образом,

(6.50)

(6.51)

где оператор 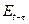обозначает ожидания на основе информации, доступной в момент времени 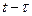. В уравнении (6.50) учтен тот факт, что цена уже определена в момент установления цены 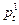, а значит, не является случайной величиной.

Наша цель состоит в определении динамики во времени уровня цен и выпуска для заданной динамики . Начнем с того, что выразим 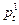в уравнении (6.50):

. (6.52)

Предположение о рациональных ожиданиях позволяет нам определить поведение индивидов, устанавливающих цены в периоде . Правая и левая часть уравнения (6.52) равны, так что ожидания правой и левой части, формируемые в периоде , также должны быть равны:

. (6.53)

В уравнении (6.53) был использован тот факт, что ожидания просто равны . В противном случае, ожидания должны были бы пересматриваться в сторону повышения или понижения. А это означало бы, что первоначально ожидания не были рациональными. Текущие ожидания относительно будущих ожиданий случайной величины равны текущим ожиданиям случайной величины. Этот факт известен как закон итерированных проекций.

Подставляя (6.53) в (6.51), получаем

. (6.54)

Выражая из данного уравнения , получаем простое определение:

. (6.55)

Теперь можно скомбинировать полученные результаты и определить равновесие. Подставляя (6.55) в (6.52) и упрощая, получаем

. (6.56)

И наконец, подставляя (6.55) и (6.56) в выражения, определяющие уровень цен и выпуск, и , окончательно получаем

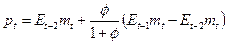, (6.57)

. (6.58)

Следствия

Уравнение (6.58) представляет основные результаты модели. Во-первых, также как и в модели Лукаса, непредвиденные сдвиги агрегированного спроса обладают реальными эффектами. Это определяется наличием слагаемого . Т.к. индивиды не знают в момент, когда они устанавливают цены, эти шоки один к одному отражаются на выпуске.

Во-вторых, и это существенно, шоки агрегированного спроса, о которых становятся известно после того, как одна половина цен уже была установлена, также воздействуют на выпуск. Рассмотрим появление информации об агрегированном спросе в периоде , которая становится известной при переходе от периода к периоду . На практике это может соответствовать появлению прогноза будущей динамики основных индикаторов экономической активности, или появлению информации о возможных изменениях в монетарной политике. Как видно из уравнений (6.57) и (6.58), доля от изменения в , ожидания которого возникают при переходе от периода к периоду , отражается на выпуске, а оставшаяся доля отражается на ценах. Причина, по которой данное изменение не оказывается нейтральным, очевидна: не все цены являются полностью гибкими в краткосрочно перспективе.

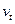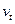Это позволяет незамедлительно сделать вывод: политика правил может стабилизировать экономику. Так же как в разделе 6.3, предположим, что равно , где - переменная подконтрольная политике, а представляет прочие шоки агрегированного спроса. Предположим, что политики обладают той же информацией, что и частные агенты, устанавливающие цены. Следовательно, они вынуждены определять до того, как величина стала известной. Тем не менее, коль скоро политические деятели могут подстроить , реагируя на информацию, раскрытую при переходе от периода к периоду , монетарная политика может стабилизировать экономику. Если 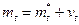, то из (6.58) вытекает, что 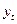зависит от и от . Подстраивая с тем расчетом, чтобы нейтрализовать , политики могут нейтрализовать воздействие на выпуск со стороны 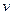даже в том случае, когда информация о 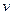является общедоступной.

Еще один важный вывод состоит в том, что взаимодействие между индивидами, устанавливающими цены, может привести как к усилению, так и к ослаблению жесткости цен, имеющей место на микроуровне. Рассмотрим шок агрегированного спроса, о котором становится известно после того как часть цен уже была установлена. Может показаться, что т.к. половина цен уже установлена, а оставшаяся половина может быть установлена совершенно свободно, то половина шока перейдет на цены, а оставшаяся половина отразится на выпуске. Уравнения (6.57) и (6.58) показывают, что в общем случае это неверно. Ключевым здесь является параметр : как показывает уравнение (6.58), доля шока, которая окажет воздействие на выпуск, равна не ½, а .

Как мы помним, в уравнении (6.45) параметр характеризовал чувствительность оптимальных реальных цен к агрегированному реальному выпуску: . Тогда можно сказать, что чем ниже значение , тем сильнее степень реальной жесткости (Ball and D. Romer, 1990). Реальная жесткость сама по себе не приводит к реальным эффектам монетарных шоков: если цены могут подстраиваться свободно, то деньги будут нейтральны в независимости от величины . Однако реальная жесткость усиливает эффект номинальной жесткости: если агенты, устанавливающие цены, не могут подстраивать их абсолютно свободно, то более высокая степень реальной жесткости (т.е. более низкое ) усиливает реальный эффект монетарного шока. Причина этого кроется в том, что чем ниже , тем в меньшей степени индивиды озабочены изменениями устанавливаемых ими относительных цен. В результате, индивиды, у которых еще есть возможность свободно подстроить свои цены, не будут их устанавливать на уровне, отличающемся существенно от уже установленных. Так что реальный эффект монетарного шока может оказаться значительным. Если же, напротив, превосходит 1, агенты, еще имеющие возможность устанавливать цены, изменят их довольно существенно, и агрегированные реальные эффекты изменений в будут слабыми.[13]

И последнее. Модель показывает, что выпуск не зависит от (для данных величин и 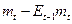). Т.е., любая информация относительно агрегированного спроса, на которую имеют возможность прореагировать все агенты, устанавливающие цены, не будет оказывать воздействие на выпуск.

Дата добавления: 2015-10-30