
|
Читайте также: |
Обозначив через  относительную цену товара
относительную цену товара 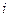 , можно записать:
, можно записать:
 (6.16)
(6.16)
Таким образом, переменная, которую может наблюдать индивид – цена его товара – равна сумме относительной цены товара и агрегированного уровня цен (в логарифмах).
Принимаемые индивидуальные решения о производстве должны основываться только на  (см. [6.6]). Однако индивид не наблюдает переменную
(см. [6.6]). Однако индивид не наблюдает переменную  и должен оценить ее на основании наблюдаемой переменной
и должен оценить ее на основании наблюдаемой переменной  .[4] Далее Лукас вводит два упрощающих предположения. Во-первых, он предполагает, что индивиды вначале строят свои ожидания относительно величины
.[4] Далее Лукас вводит два упрощающих предположения. Во-первых, он предполагает, что индивиды вначале строят свои ожидания относительно величины  для данной величины
для данной величины  , а затем выбирают такой объем производства, как если бы построенная оценка
, а затем выбирают такой объем производства, как если бы построенная оценка  была детерминированной. Тогда уравнение (6.6) принимает вид:
была детерминированной. Тогда уравнение (6.6) принимает вид:
 . (6.17)
. (6.17)
Как показывает задача 6.1, данное поведение, построенное по принципу эквивалентности детерминированному случаю, отличается от максимизации ожидаемой полезности: вообще говоря, выбор, максимизирующий ожидаемую полезность, зависит не только от оценки индивидом величины  , но также и от того, насколько неопределенной он считает эту величину. Однако предположение о том, что индивиды используют принцип эквивалентности, не искажает основные результаты модели, упрощая при этом анализ.
, но также и от того, насколько неопределенной он считает эту величину. Однако предположение о том, что индивиды используют принцип эквивалентности, не искажает основные результаты модели, упрощая при этом анализ.
Во-вторых, (и это очень важно) Лукас предполагает, что индивиды формируют ожидание  при данном
при данном  рациональным образом. Т.е., предполагается, что
рациональным образом. Т.е., предполагается, что  - это среднее значение
- это среднее значение  , исчисляемое на основе информации о
, исчисляемое на основе информации о  и о совместном распределении двух этих переменных*. На сегодняшний день, предположение о рациональных ожиданиях кажется не менее привычным, чем предположение о максимизации индивидом функции полезности. Однако, в то время, когда Лукас ввел в макроэкономический анализ гипотезу рациональных ожиданий, предложенную в работах Muth (1960, 1961), она воспринималась как весьма спорная. Как мы увидим ниже, это один из источников (хотя и далеко не единственный) основных результатов модели Лукаса.
и о совместном распределении двух этих переменных*. На сегодняшний день, предположение о рациональных ожиданиях кажется не менее привычным, чем предположение о максимизации индивидом функции полезности. Однако, в то время, когда Лукас ввел в макроэкономический анализ гипотезу рациональных ожиданий, предложенную в работах Muth (1960, 1961), она воспринималась как весьма спорная. Как мы увидим ниже, это один из источников (хотя и далеко не единственный) основных результатов модели Лукаса.
Чтобы упростить вычисления  , монетарные шоки (
, монетарные шоки ( ) и шоки индивидуального спроса на товары (
) и шоки индивидуального спроса на товары ( ) полагаются нормально распределенными. Величина
) полагаются нормально распределенными. Величина  имеет среднее
имеет среднее  и дисперсию
и дисперсию  . Величины
. Величины  имеют нулевое среднее, дисперсию
имеют нулевое среднее, дисперсию  и полагаются независимыми от
и полагаются независимыми от  . Как мы увидим, из этих предположений следует, что величины
. Как мы увидим, из этих предположений следует, что величины 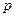 и
и  являются независимыми и нормально распределенными. Т.к.
являются независимыми и нормально распределенными. Т.к.  равна
равна  , эта величина также будет нормально распределенной со средним, равным сумме средних
, эта величина также будет нормально распределенной со средним, равным сумме средних 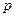 и
и  , и дисперсией, равной сумме дисперсий этих переменных. Также мы увидим, что средние
, и дисперсией, равной сумме дисперсий этих переменных. Также мы увидим, что средние 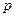 и
и  ,
,  и
и  , равны, соответственно,
, равны, соответственно,  и 0, а их дисперсии
и 0, а их дисперсии 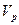 и
и 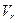 - это сложные функции от
- это сложные функции от  ,
,  и других параметров модели.
и других параметров модели.
Задача индивида состоит в построении ожидания  при данном
при данном  . Один из важных результатов математической статистики состоит в том, что в случае, когда две переменных имеют совместное нормальное распределение (как
. Один из важных результатов математической статистики состоит в том, что в случае, когда две переменных имеют совместное нормальное распределение (как  и
и  в данной ситуации), ожидание одной из переменных является линейной функцией от наблюдаемого значения второй. Таким образом,
в данной ситуации), ожидание одной из переменных является линейной функцией от наблюдаемого значения второй. Таким образом,  может быть представлено в виде:
может быть представлено в виде:
 . (6.18)
. (6.18)
В данном частном случае, когда  равно
равно  плюс независимая случайная величина, (6.18) принимает конкретную форму:
плюс независимая случайная величина, (6.18) принимает конкретную форму:
 (6.19)
(6.19)
Смысл уравнения (6.19) понятен интуитивно. Во-первых, получается, что если  совпадает со своим средним, то и ожидаемая величина
совпадает со своим средним, то и ожидаемая величина  будет равна своему среднему, т.е. 0. Во-вторых, ожидаемая величина
будет равна своему среднему, т.е. 0. Во-вторых, ожидаемая величина  превосходит среднее тогда, когда
превосходит среднее тогда, когда  превосходит свое среднее, и оказывается ниже среднего, в ситуации, когда
превосходит свое среднее, и оказывается ниже среднего, в ситуации, когда  ниже среднего. В третьих, доля в отклонении
ниже среднего. В третьих, доля в отклонении  от своего среднего, объясняемая отклонением
от своего среднего, объясняемая отклонением  от своего среднего, равна
от своего среднего, равна  . И это есть не что иное, как доля общей дисперсии
. И это есть не что иное, как доля общей дисперсии  , равной
, равной  , объясняемая дисперсией
, объясняемая дисперсией  , т.е.
, т.е. 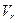 . Так например, если
. Так например, если 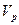 равно 0, то вся вариация случайной величины
равно 0, то вся вариация случайной величины  обусловлена вариацией
обусловлена вариацией  , так что
, так что  равно
равно  . А если
. А если 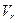 и
и 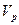 равны, то половина дисперсии
равны, то половина дисперсии  объясняется дисперсией
объясняется дисперсией  , так что
, так что  . И т.д.[5]
. И т.д.[5]
Подставляя (6.19) в (6.17), получаем индивидуальное предложение труда:
 (6.20)
(6.20)
Усредняя (6.20) по производителям и используя определения  и
и 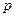 , получаем выражение для агрегированного выпуска:
, получаем выражение для агрегированного выпуска:
 (6.21)
(6.21)
Уравнение (6.21) описывает кривую предложения Лукаса. В соответствии с ним, отклонение выпуска от своего нормального уровня (равного нулю в данной модели) является возрастающей функцией от неожиданного отклонения уровня цен.
Кривая предложения Лукаса, по существу, совпадает с представленной в главе 5 модифицированнойкривой Филлипса, где базовая инфляция заменена на инфляционные ожидания (см. уравнение [5.38]). Оба подхода предполагают, что если не брать в расчет шоки предложения, выпуск становится выше равновесного только в ситуации, когда инфляция (и, следовательно, уровень цен) выше ожидаемого уровня. Таким образом, модель Лукаса подводит микроэкономическое основание под данный взгляд на агрегированное предложение.
Равновесие
Рассматривая совместно кривую предложения Лукаса (уравнение [6.21]) и кривую агрегированного спроса (уравнение [6.10],  ) находим решения для
) находим решения для 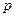 и
и  :
:
 , (6.22)
, (6.22)
 . (6.23)
. (6.23)
Далее, используя (6.22), можно найти  . Ex post, после того как величина
. Ex post, после того как величина  становится известной, правая и левая часть (6.22) должны быть равны. Тогда ex ante, до того как
становится известной, правая и левая часть (6.22) должны быть равны. Тогда ex ante, до того как  становится известной, ожидания правой и левой части должны быть равны:
становится известной, ожидания правой и левой части должны быть равны:
 , (6.24)
, (6.24)
или
 . (6.25)
. (6.25)
Используя (6.25) и тот факт, что  , уравнения (6.22) и (6.23) можно переписать в виде:
, уравнения (6.22) и (6.23) можно переписать в виде:
 , (6.26)
, (6.26)
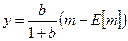 . (6.27)
. (6.27)
Уравнения (6.26) и (6.27) представляют основные результаты модели: наблюдаемая компонента агрегированного спроса,  , воздействует только на цены, а ненаблюдаемая компонента,
, воздействует только на цены, а ненаблюдаемая компонента, 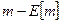 , обладает реальным эффектом. Например, рассмотрим неожиданное увеличение
, обладает реальным эффектом. Например, рассмотрим неожиданное увеличение  , т.е. реализацию
, т.е. реализацию  на уровне выше ожидаемого среднего при данном распределении. Рост предложения денег увеличивает агрегированный спрос, а значит, приводит к сдвигу вправо кривой спроса на каждое благо. Т.к. рассматриваемое изменение является ненаблюдаемым, то каждый производитель будет считать, что имеющий место рост спроса на его товар частично отражает шок относительных цен. Таким образом, производители увеличат выпуск.
на уровне выше ожидаемого среднего при данном распределении. Рост предложения денег увеличивает агрегированный спрос, а значит, приводит к сдвигу вправо кривой спроса на каждое благо. Т.к. рассматриваемое изменение является ненаблюдаемым, то каждый производитель будет считать, что имеющий место рост спроса на его товар частично отражает шок относительных цен. Таким образом, производители увеличат выпуск.
Эффекты наблюдаемого увеличения  существенно отличаются. Например, рассмотрим эффекты сдвига вверх всего распределения
существенно отличаются. Например, рассмотрим эффекты сдвига вверх всего распределения  , при неизменной реализации
, при неизменной реализации 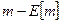 . В данном случае каждый производитель относит рост спроса на свою продукцию к последствиям роста денежной массы, а значит, не будет менять объем производства. При этом, конечно, шоки вкусов и предпочтений приводят к изменению относительных цен и объемов выпуска разных товаров, также как это имело место в случае ненаблюдаемых шоков. Однако в среднем реальный выпуск при этом не меняется. Таким образом, наблюдаемые шоки агрегированного спроса воздействуют только на цены.
. В данном случае каждый производитель относит рост спроса на свою продукцию к последствиям роста денежной массы, а значит, не будет менять объем производства. При этом, конечно, шоки вкусов и предпочтений приводят к изменению относительных цен и объемов выпуска разных товаров, также как это имело место в случае ненаблюдаемых шоков. Однако в среднем реальный выпуск при этом не меняется. Таким образом, наблюдаемые шоки агрегированного спроса воздействуют только на цены.
В завершении, мы должны выразить коэффициент  в терминах исходных параметров модели, а не в терминах дисперсий
в терминах исходных параметров модели, а не в терминах дисперсий 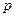 и
и  . В соответствии с уравнением (6.20),
. В соответствии с уравнением (6.20),  . Из уравнения (6.26) вытекает, что
. Из уравнения (6.26) вытекает, что  . Уравнение спроса (6.7) и уравнение предложения (6.21) можно использовать в определении
. Уравнение спроса (6.7) и уравнение предложения (6.21) можно использовать в определении 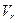 , дисперсии
, дисперсии  . А именно, подставляя
. А именно, подставляя  в уравнение (6.7) мы получим
в уравнение (6.7) мы получим  . Кроме того, можно переписать (6.20) в виде
. Кроме того, можно переписать (6.20) в виде  . Выражая
. Выражая  из последних двух уравнений, имеем
из последних двух уравнений, имеем  . Таким образом, мы получаем, что
. Таким образом, мы получаем, что  .
.
Подставляя полученные выражения для 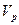 и
и 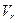 в уравнение (6.20), определяющее
в уравнение (6.20), определяющее  , получаем:
, получаем:
 . (6.28)
. (6.28)
Уравнение (6.28) определяет коэффициент  в терминах
в терминах  ,
,  и
и  . Таким образом, теперь модель построена до конца. Несложно показать, что
. Таким образом, теперь модель построена до конца. Несложно показать, что  возрастает с ростом
возрастает с ростом  и убывает с ростом
и убывает с ростом  . В частном случае, когда
. В частном случае, когда  , мы можем получить аналитическое решение для
, мы можем получить аналитическое решение для  :
:
 . (6.29)
. (6.29)
И, наконец, из того, что  и
и  , следует, что
, следует, что 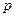 и
и  являются линейными функциями от
являются линейными функциями от  и
и  . Т.к.
. Т.к.  и
и  являются независимыми,
являются независимыми, 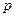 и
и  также будут независимыми. Линейная функция нормально распределенных случайных величин сама является нормально распределенной случайной величиной. Следовательно,
также будут независимыми. Линейная функция нормально распределенных случайных величин сама является нормально распределенной случайной величиной. Следовательно, 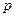 и
и  имеют нормальное распределение. Это подтверждает обоснованность введенных выше предположений относительно данных переменных.
имеют нормальное распределение. Это подтверждает обоснованность введенных выше предположений относительно данных переменных.
Дата добавления: 2015-10-30; просмотров: 118 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Поведение производителей | | | Кривая Филлипса и критика Лукаса |