Метод неопределенных коэффициентов

Как обсуждалось в разделе 4.6, основная идея метода неопределенных коэффициентов состоит в подборе общей функциональной формы решения с последующим поиском конкретных значений коэффициентов на основе самой модели. В рассматриваемой здесь модели, в периоде две переменные уже даны – это денежная масса, , и установленные в предшествующем периоде цены, . Кроме того, модель является линейной. Так что вполне оправданной будет пробное предположение, что должна быть линейной функцией от и :

. (6.63)

Наша задача состоит в определении значений , и , которые решают данную модель.

Перед тем как приступить к поиску , и , можно упростить вычисления, если вначале использовать наше знание модели для того, чтобы дополнительно ограничить (6.33). Мы нормализовали к нулю константу в уравнении, определяющем оптимальные цены, . Как следствие, в равновесии с гибкими ценами должно быть равным 0, а все цены должны быть равны . С учетом этого, рассмотрим ситуацию, когда и равны. Если в периоде индивиды, устанавливающие цены, также установят их на уровне , то экономика окажется в равновесии с гибкими ценами. Кроме того, т.к. следует процессу случайного блуждания, у индивидов, устанавливающих цены в периоде , нет оснований полагать, что будет в среднем выше или ниже чем . Следовательно, будет в среднем соответствовать . Так что в данной ситуации и будут равны , и индивиды установят цены . Для (6.63) это означает, что

(6.64)

для любых .

Для соблюдения (6.64) требуется выполнение двух условий. Во-первых, должно соблюдаться . В противном случае (6.64) не будет верно для любых . Во-вторых, если мы установим , соблюдение (6.64) дополнительно потребует, чтобы . Подставляя данные условия в (6.63), получаем:

. (6.65)

Наша задача теперь состоит в поиске значения , решающего модель.

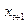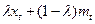Уравнение (6.65) может быть записано для любого периода. В частности, . Тогда формируемые в периоде ожидания - это ожидания , что просто равно . Подставляя в последнее выражение из (6.65), получаем:

(6.66)

В свою очередь, подстановка полученного выражения в (6.62) дает:

(6.67)

Если агенты, устанавливающие цены, верят в то, что является линейной функцией от и в форме, предполагаемой (6.65), то, максимизируя прибыль, они действительно будут устанавливать свои цены как линейные функции от данных переменных. Если мы найдем решение модели, два данных линейных уравнения должны быть одинаковыми. Сравнивая (6.65) и (6.67), можно сделать вывод, что для их совпадения требуется выполнение двух условий:

, (6.68)

и

. (6.69)

Уравнение (6.68) является квадратным по . Его решение определяется корнями

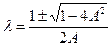. (6.70)

Несложно показать, что эти значения удовлетворяют также и условию (6.69). С учетом определения константы в (6.62), значения можно переписать в виде:

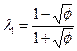, (6.71)

. (6.72)

Однако, имеет смысл рассматривать только одно из значений , а именно . Если , то . Экономическая динамика при этом будет устойчивой. Напротив, в случае, когда . Динамика экономики будет при этом неустойчивой: незначительный шок устремит выпуск в плюс или минус бесконечность. В результате, предположения, положенные в основу модели (например, предположение, что продавцы не рационируют покупателей) не будут соблюдаться. По этой причине, мы рассмотрим лишь величину .

Таким образом, выражение (6.65) для является решением модели: если индивиды, устанавливающие цены, верят, что другие используют то же самое правило, они сами будут считать рациональным использовать именно его.

Теперь мы можем описать динамику выпуска. Величи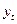на равна , что в свою очередь равно . С учетом уравнения динамики , (6.65), получаем:

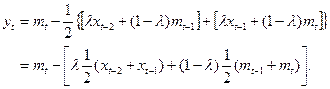(6.73)

Используя то, что , и тот факт, что 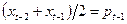, последнее выражение можно свести к следующему простому виду:

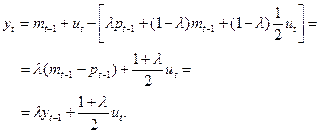(6.74)

Следствия

Уравнение (6.74) представляет основные результаты модели. Т.к. является положительной величиной (что верно в случае, если 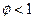), из уравнения (6.74) следует, что шоки агрегированного спроса будут характеризоваться продолжительными эффектами на выпуск – эффектами, которые будут наблюдаться даже после того как все индивиды изменят свои цены. Предположим, что экономика первоначально находится в состоянии равновесия с гибкими ценами (т.е. находится на стационарном нулевом уровне), и рассмотрим эффект положительного шока 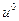. В период времени, когда происходит данный шок, не все индивиды могут подстроить свои цены, так что вполне естественно, что при этом возрастает. Как следует из (6.74), . В следующем периоде, несмотря на то, что теперь оставшиеся индивиды могут подстроить цены, не возвращается к своему нормальному уровню даже в отсутствии новых шоков: в соответствии с (6.74), 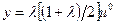. И так постепенно выпуск возвращается к своему нормальному уровню, при условии, что на каждом этапе.

Реакция уровня цен на шок представляет собой как бы обратную сторону реакции выпуска. Уровень цен возрастает на в первом периоде, а затем на долю оставшегося расстояния от 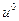в каждом последующем периоде. Таким образом, в экономике будет наблюдаться инерция уровня цен.

Источником продолжительных реальных эффектов монетарных шоков вновь выступает нежелание индивидов в полной мере менять свои относительные цены. Вспомним, что , и что 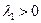только в случае, когда 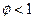. Так что плавная подстройка цен будет иметь место, только если оптимальные цены являются возрастающей функцией уровня цен. Предположим, что каждый индивид решает полностью подстроить свою цену при первой же возможности. В данном случае, индивиды, устанавливающие цены в периоде, когда происходит шок, сразу же подстроят свои цены на всю величину шока. Оставшиеся индивиды сделают то же в следующем периоде. Таким образом, вырастет на величину в начальном периоде и вернется к своему нормальному уровню в следующем периоде.

Однако представленная быстрая подстройка не может иметь место в равновесии в случае, когда меньше 1. Действительно, рассмотрим индивидов, подстраивающих свои цены сразу же. Как предполагается, все цены будут подстроены ко второму периоду, так что для данного периода каждый индивид выбирает оптимальную цену. Но если 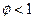, то оптимальная цена будет низкой, когда уровень цен низкий. Не все цены могут подстроиться сразу же в ответ на шок. Так что цены, подобранные оптимальным образом в период, когда происходит шок, будут ниже оптимального уровня в следующем периоде. Получается, что данным индивидам не имеет смысла полностью подстраивать цены в первоначальном периоде. Но это в свою очередь означает, что оставшимся индивидам также будет невыгодно полностью приспосабливать свои цены в следующем периоде. И знание, что полная подстройка не будет наблюдаться и в будущем сдерживает реакцию индивидов, подстраивающих свои цены в период когда происходит шок. Окончательным результатом описанного вперед и назад смотрящего взаимодействия будет плавный процесс подстройки, представленный уравнением (6.65).

Таким образом, также как и в модели, где цены предопределены, но не фиксированы, степень неполноты номинальной подстройки на уровне агрегатов может оказаться сильнее, чем можно было бы предположить первоначально лишь на том основании, что не все цены подстраиваются в каждом периоде. Действительно, степень негибкости агрегированного уровня цен будет еще выше в данной ситуации, когда наблюдается последействие даже после того, как все цены изменились. И снова низкое значение , т.е. высокая степень реальной жесткости, является необходимым для данного результата условием. Если равно 1, т.е. равно 0, то каждый индивид будет полностью подстраивать свою цену при первой же возможности. Если превышает 1, то является отрицательным, так что 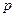изменяется сильнее, чем в период, следующий за шоком, и процесс возвращения к долгосрочному равновесию будет носить характер колебаний.

Дата добавления: 2015-10-30