Приведение квадратичной формы к главным осям.

Пусть 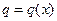— квадратичная форма в .

Теорема. В найдётся ортонормированный базис , в котором имеет вид .

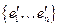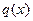Пусть — произвольный ортонормированный базис в пространстве , и — матрица в этом базисе. Тогда , и, значит, существует линейный самосопряжённый оператор с матрицей . По предыдущей теореме существует ортонормированный базис из собственных векторов , в котором имеет диагональную матрицу . Значит . По лемме 3 , поэтому — диагональна. Но — матрица в .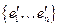

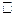
Опр. Приведением квадратичной формы к главным осям называют переход к ортогональному базису в , где она имеет нормальный вид.

ОРТОГОНАЛЬНЫЕ ОПЕРАТОРЫ

Основные понятия

Пусть — линейный оператор в евклидовом пространстве .

Опр. Оператор ортогонален, если он сохраняет скалярное произведение, то есть .

Лемма 4. ортогонален имеет ортогональную матрицу в ортонормированном базисе.

Пусть — ортонормированный базис , — матрица в этом базисе, , . Тогда . Поэтому ортогонален .

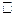
Лемма 5. Пусть — ортогональный оператор на евклидовом пространстве 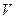, — инвариантное подпространство для . Тогда и 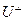также инвариантно для .

По лемме 4 оператор — не вырожден. Тогда , и значит . Поэтому . Пусть — любой вектор, . Тогда и

, то есть .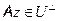

12 марта 2005

Канонический базис для ортогонального оператора.

Теорема. Пусть — ортогональный оператор в . Тогда существует ортонормированный базис, в котором матрица имеет вид:

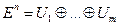(1) По лемме 1 (см. самосопряжённые операторы) у есть инвариантное подпространство . По лемме 5: . Следовательно, — инвариантные подпространства, или . Кроме того, не содержат инвариантных подпространств 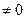и . При этом .

(2) Пусть . Тогда и .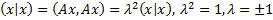

(3) , — ортонормированный базис , — матрица в этом базисе, 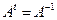по лемме 4. Тогда .

(а) Предположим, что . Вычислим :

. Отсюда корни на — вещественные, следовательно, существует собственный вектор в в есть 1-мерное — инвариантное подпространство. Противоречие.

(б) остался случай . Тогда

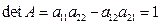, поэтому . Значит, система имеет единственное решение. Подходит .

Дата добавления: 2015-10-26