Ортогональные дополнения

Опр.

Свойство 1: 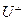- подпространство

Свойство 2:

Теорема. Пусть 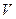- конечномерное евклидово пространство. Тогда для любого подпространства выполнено равенство:

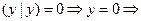
Если , то и 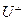не пересекаются 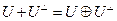. Пусть - ортонормированный базис и 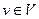. Положим , и . Тогда , т.е. и

Следствие. . Если , то

8. Сопряжённые операторы

Пусть 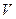— евклидово пространство, .

Опр. сопряжён к (обозначается ), если .

Таким образом, по определению . Существование для любого оператора сопряжённого, докажем чуть позже.

Предложение. 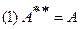и

(1).

а значит, по предыдущей теореме .

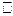
(2). .

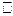
Теорема. Пусть — матрица оператора в ортонормированном базисе . Тогда имеет в этом базисе матрицу .

Обозначим . Пусть — матрица в базисе . Тогда:

, . Непосредственно из определения и ортонормированности базиса следует, что . Итак, доказано, что .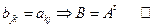

Замечание. Мы ещё не доказали существование сопряжённого оператора для любого, но это очевидно (достаточно положить = и провести аналогичное доказательство).

9. Самосопряжённые операторы

Опр. Оператор самосопряжён в евклидовом пространстве 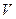, если .

Лемма 1. Пусть — линейный оператор на 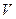над и . Тогда существует ненулевое инвариантное подпространство размерности меньше 2 (т.е. и ).

Если имеет собственный вектор , то — это инвариантное подпространство размерности 1, и всё доказано. Так что будем считать, что собственных векторов у нет. Рассмотрим минимальный многочлен : . В его разложении на множители над будут множители степени 2 и только они (если есть множитель степени 1, то есть и собственный вектор, противоречие). Выделим один из них. Таким образом и 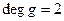. Рассмотрим оператор 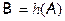. Так как , то многочлен не минимальный и, значит, . Пусть , а и . Пусть . Тогда . Осталось доказать лишь, что , то есть, что . Пусть . Тогда . Однако, из определения , . Отсюда .

Лемма 2. Пусть — самосопряжённый оператор на евклидовом пространстве , 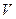— инвариантное подпространство для . Тогда и также инвариантно для .

, . Итак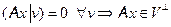

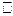
Теорема. Пусть — самосопряжённый оператор на евклидовом пространстве . Тогда в 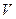существует ортонормированный базис из собственных векторов .

Индукция по . — очевидно.

Пусть (именно этот случай мы будем использовать в шаге), — ортонормированный базис V, — матрица оператора в этом базисе. Из самосопряжённости , следует, что:

.

у есть хоть один действительный корень у есть собственный вектор . Но , а также инвариантно по лемме 2. Отсюда базис — искомый базис.

Пусть . По лемме 1 существует , . Тогда , а значит , где .

Опр. Матрица называется ортогональной, если 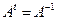, то есть .

Лемма 3. Матрица перехода от одного ортонормированного базиса в к другому ортогональна.

Пусть и 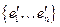— два ортонормированных базиса. Пусть — матрица перехода от первого ко второму базису. Тогда . Из ортонормированности следует, что . С другой стороны, , что и означает, что .

Дата добавления: 2015-10-26