Матрица линейного оператора.

Пусть – базис пространства V, и .

Опр. Если , то матрица в базисе

(j-й столбец А – координаты вектора в базисе )

Переход к другому базису.

Пусть и - два базиса V, , A – матрица в базисе , B – матрица в базисе , Пусть С – матрица переход а от к , т.е.

Теорема.

Посчитаем двумя способами:

1)

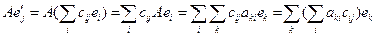
2)

Отсюда , т.е. , значит СВ=АС, т.к. С – невырождена, то

Определитель и след линейного оператора.

Предложение. Определитель и след матрицы линейного оператора не зависят от выбора базиса.

Определение.

Оператор – невырожденный, если det A 0.

Критерий невырожденности – невырожденный Ker = 0 Im = V rank A = dim V

Инвариантные подпространства.

Пусть – линейный оператор на V и .

Опр. U называется инвариантным подпространством для , если (т.е. )

Пусть – базис U, k≤n. Дополним его до базиса V .
Тогда , причем , т.е. матрица А имеет в базисе вид .

Если и 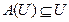, , то существует базис V, в котором .

Собственные векторы, собственные значения.

Опр. – собственный вектор оператора , если существует скаляр такой, что ; тогда – собственное значение.

Свойство. V – собственный вектор – инвариантное подпространство.

Теорема. Число является собственным значением оператора тогда и только тогда, когда , где Е – тождественный оператор на V. (то есть для любого х 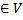E(х) = х)

1) Пусть v – собственный вектор, 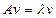. Зафиксируем базис в V. Если Х – столбец координат v в этом базисе, то 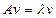(где А – матрица в ) , где Е – единичная матрица. Следовательно, если собственное значение равно , то

(Примечание: не стоит путать обозначения A и A(хотя они и очень похожи.). Курсивом обозначен оператор, а обычным шрифтом --- матрица. Также E --- это тождественный оператор, а Е --- это единичная матрица.)

2) Пусть , тогда (А, Е – матрицы , Е в базисе ) система имеет ненулевое решение вектор – собственный,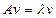

ХАРАКТЕРИСТИЧЕСКИЙ МНОГОЧЛЕН ОПЕРАТОРА

Определения

А – матрица оператора в некотором базисе пр-ва V.

Опр. Многочлен от переменной t называют многочленом оператора А.

не зависит от выбора базиса: если В – матрица А в другом базисе, то и .

Опр. Характеристический корень оператора: – характеристический корень, если .

Замечание. – характеристический корень – собственное значение оператора.

Дата добавления: 2015-10-26