
Пусть  , U – подпространство в V.
, U – подпространство в V.
Опр. Множество точек 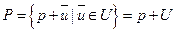 называют аффинным подпространством (или плоскостью в A) размерностью
называют аффинным подпространством (или плоскостью в A) размерностью  . Говорят, что U – направляющее подпространство для P.
. Говорят, что U – направляющее подпространство для P.
Предложение. Подпространство P является аффинным подпространством, ассоциированным с U.
Пусть  ,
,  . Тогда
. Тогда  и
и  . Далее, пусть
. Далее, пусть  . Тогда
. Тогда 
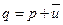 . Пусть также
. Пусть также  ,
,  ,
,  . Тогда
. Тогда 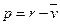 и
и  , т.е.
, т.е. 
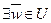 :
:  . Единственность очевидна.
. Единственность очевидна. 
Направляющее пространство U однозначно определяется по P.
Опр. Прямая – подпространство размерности 1.
Прямая, проходящая через  :
: 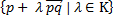
Теорема. Подмножество  является подпространством
является подпространством  P содержит прямую, проходящую через любые 2 точки
P содержит прямую, проходящую через любые 2 точки  .
.
(1) Пусть сначала P – плоскость,  .
.
Пусть  ,
, 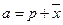 ,
,  . Тогда
. Тогда  и
и  ,
, 

 .
.
(2) Обратно, пусть P содержит все прямые.
Возьмем любую точку  . Обозначим
. Обозначим  . Докажем, что U – подпространство в V.
. Докажем, что U – подпространство в V.
Пусть  . Тогда
. Тогда  . Но
. Но  , поэтому
, поэтому  , т.е.
, т.е.  для
для  . Достаточно теперь доказать, что
. Достаточно теперь доказать, что  для любых
для любых  . Но это следует из того, что P содержит прямую pq для любой точки p: если
. Но это следует из того, что P содержит прямую pq для любой точки p: если  , то
, то  , т.е.
, т.е. 
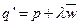 и
и 

Следствие. Если  и
и  - плоскости в A, то их пересечение
- плоскости в A, то их пересечение  либо пусто, либо является плоскостью с направляющим подпространством
либо пусто, либо является плоскостью с направляющим подпространством  , где
, где  – направляющие подпространства для
– направляющие подпространства для  и
и  .
.
Если P содержит ровно одну точку, то это 0-мерное подпространство с  . Если
. Если  , то, по теореме, P содержит прямую ab
, то, по теореме, P содержит прямую ab  P – подпространство.
P – подпространство.
Зафиксируем точку  . Тогда, если
. Тогда, если  , то
, то  , т.е.
, т.е.  . Поэтому
. Поэтому  . Обратное включение очевидно.
. Обратное включение очевидно. 
Опр. Плоскости 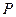 и
и  называются параллельными, если они имеют одно и тоже направляющее подпространство U, т.е.
называются параллельными, если они имеют одно и тоже направляющее подпространство U, т.е.  .
.
Обобщение.  , P параллельно Q, если
, P параллельно Q, если  или
или  .
.
Опр. Плоскости P и Q называются скрещивающимися, если они не параллельны, но  .
.
Опр. Точки 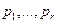 называются точками общего положения, если они не лежат ни в одной плоскости размерности r-2.
называются точками общего положения, если они не лежат ни в одной плоскости размерности r-2.
Само K можно рассматривать как 1-мерное аффинное пространство. Поэтому можно рассматривать аффинно-линейное отображение 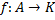 , т.е.
, т.е.  , где
, где  , т.е.
, т.е.  .
.
Если  – система координат в
– система координат в  и
и  – координаты точки P, то обозначив
– координаты точки P, то обозначив  ,
,  (
( ), получим:
), получим:
 , т.е. любое линейное уравнение
, т.е. любое линейное уравнение  можно рассматривать как уравнение
можно рассматривать как уравнение  в аффинном пространстве А размерности n, где
в аффинном пространстве А размерности n, где 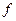 – аффинно-линейная функция.
– аффинно-линейная функция.
Теорема. Множество точек аффинного пространства, удовлетворяющих совместной системе линейных уравнений ранга r, образуют (n-r)-мерную плоскость  . Любая плоскость может быть получена.
. Любая плоскость может быть получена.
(1) Сопоставим системе  n аффинно-линейных функций.
n аффинно-линейных функций.
Зафиксируем систему координат  в
в  и положим
и положим  , где
, где  , тогда
, тогда  и
и  . Пусть совместна и
. Пусть совместна и  – ее решение. Возьмем точку
– ее решение. Возьмем точку  с координатами
с координатами  . Будем говорить, что точка p с координатами
. Будем говорить, что точка p с координатами  решение нашей системы, если
решение нашей системы, если  . Тогда
. Тогда  – решение, а вектор
– решение, а вектор  – решение однородной системы
– решение однородной системы  (*).
(*).
Т.к. совокупность решений (*) – подпространство  , а любое решение неоднородной системы получается из
, а любое решение неоднородной системы получается из  прибавлением решений однородной системы, то множество точек p, для которых
прибавлением решений однородной системы, то множество точек p, для которых  равно
равно  , т.е. это плоскость и
, т.е. это плоскость и  .
.
(2) Пусть теперь P – плоскость в А,  .
.  система уравнений
система уравнений  ,
,  , задающая U, где
, задающая U, где  – координаты вектора в некотором базисе
– координаты вектора в некотором базисе  пространства
пространства 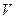
 .
.
Рассмотрим систему координат  в
в  . Тогда
. Тогда 



 ,
,  , где
, где  – координаты p в выбранной системе координат. Обозначим
– координаты p в выбранной системе координат. Обозначим 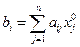 получим необходимую совместную систему линейных уравнений.
получим необходимую совместную систему линейных уравнений.
28.03.05
Дата добавления: 2015-10-26; просмотров: 181 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Унитарные операторы. | | | Доказательство. |