
Теорема 2. ЖНФ матрицы A единственна с точностью до перестановки клеток.
Пусть A – жорданова матрица n x n.  , где
, где  - жордановы клетки.
- жордановы клетки.
Обозначим:  - число клеток Jm,l среди
- число клеток Jm,l среди  . Сначала выведем формулу для
. Сначала выведем формулу для  . Пусть A: V®V – линейный оператор на n-мерном пространстве с матрицей A.
. Пусть A: V®V – линейный оператор на n-мерном пространстве с матрицей A.
Обозначим: 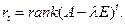 Тогда
Тогда  Здесь
Здесь  - единичные матрицы соответствующих размеров.
- единичные матрицы соответствующих размеров.
1) Если 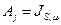 и
и  , то
, то  размер (Aj).
размер (Aj).
2) Если  , то
, то  - матрица нильпотентного оператора B = A - lE
- матрица нильпотентного оператора B = A - lE  на циклическом (для B) подпространстве U. Вычислим
на циклическом (для B) подпространстве U. Вычислим 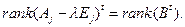 Пусть v, Bv, …, Bs-1v – циклический базис для B в U. Тогда Bt(U) = < Btv, …, Bs-1v> (или 0, если
Пусть v, Bv, …, Bs-1v – циклический базис для B в U. Тогда Bt(U) = < Btv, …, Bs-1v> (или 0, если  ). Отсюда
). Отсюда  , если t < s и u = 0 если
, если t < s и u = 0 если  .
.
3) Найдем разность  для A. Пусть
для A. Пусть  - размеры всех клеток среди
- размеры всех клеток среди  с собственным числом l. Тогда для клеток
с собственным числом l. Тогда для клеток 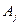 с числом
с числом  имеем
имеем  разность
разность  можно считать только по клеткам с
можно считать только по клеткам с  . Поэтому
. Поэтому 


 Т.е.
Т.е.  - число клеток Jm,l среди
- число клеток Jm,l среди  , у которых
, у которых 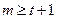 . Отсюда
. Отсюда  ) - (
) - (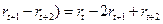 - число клеток Jk+1,l Þ формула
- число клеток Jk+1,l Þ формула  , где
, где 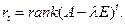
Пусть A и D матрицы двух жордановых нормальных форм одного оператора с матрицей В. Тогда: 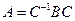 (
( - некоторая матрица),
- некоторая матрица), 

 . Поэтому
. Поэтому 
 (т.к. F является невырожденной). Преобразование мы использовали следующее:
(т.к. F является невырожденной). Преобразование мы использовали следующее:  . Таким образом,
. Таким образом,  . Это и есть единственность. ð
. Это и есть единственность. ð
28.02.05
БИЛИНЕЙНЫЕ ФОРМЫ
Определение.
F – поле, V – векторное пространство над эти полем.
Опр. Функция  называется билинейной формой, если она линейна по каждому аргументу. То есть:
называется билинейной формой, если она линейна по каждому аргументу. То есть:
1) 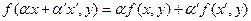
2) 
Матрица билинейной формы.
Пусть 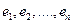 - базис V. Обозначим
- базис V. Обозначим  .
.
Опр.  называют матрицей билинейной формы f в базисе
называют матрицей билинейной формы f в базисе 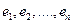 .
.
Координатная запись.  ,
, 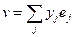 . Тогда:
. Тогда:
 , где
, где
 ,
,  ,
,  , а
, а  .
.
Изменение матрицы билинейной формы при замене базиса.
Пусть  и
и  - два базиса пространства V. Пусть С – матрица перехода от базиса
- два базиса пространства V. Пусть С – матрица перехода от базиса  к базису
к базису  . Пусть
. Пусть

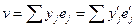
Тогда:
 ,
,  . Отсюда
. Отсюда
 , где
, где  - матрица
- матрица  в базисе
в базисе  . С другой стороны
. С другой стороны 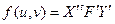 , где
, где 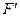 - матрица
- матрица  в базисе
в базисе  .
.
Замечание. Если для любых столбцов  выполняется равенство
выполняется равенство  , то матрицы В и А равны.
, то матрицы В и А равны.
Пусть  ,
, 
(в смысле, что единица стоит на i-ом и j-ом месте соответственно; ни в коем случае не подразумевается вычитание) 
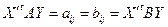 .
.
Учитывая замечание, получаем:  .
.
Дата добавления: 2015-10-26; просмотров: 150 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Матрица линейного оператора. | | | Квадратичные формы |