
Читайте также:
|
Интегрирование рациональной функции после выделения целой части сводится к интегрированию правильной рациональной дроби:
1 вид:  , где
, где  и
и 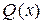 - целые многочлены, причем степень числителя ниже степени знаменателя. Если
- целые многочлены, причем степень числителя ниже степени знаменателя. Если
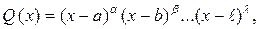 (2.3.1)
(2.3.1)
где  - различные действительные корни многочлена;
- различные действительные корни многочлена;  - натуральные числа (кратности корней), то справедливо разложение рациональной дроби
- натуральные числа (кратности корней), то справедливо разложение рациональной дроби  с помощью неопределенных коэффициентов на простейшие дроби:
с помощью неопределенных коэффициентов на простейшие дроби:
 (2.3.2)
(2.3.2)
Замечание 2.3.1. Для вычисления неопределенных коэффициентов  обе части тождества (2.3.2) приводят к общему знаменателю, а затем, поскольку получают равные дроби с одинаковыми знаменателями, а значит и с равными числителями, то приравнивают числители. Из курса алгебры известно, что два многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях переменной х, поэтому их следует приравнять.
обе части тождества (2.3.2) приводят к общему знаменателю, а затем, поскольку получают равные дроби с одинаковыми знаменателями, а значит и с равными числителями, то приравнивают числители. Из курса алгебры известно, что два многочлена равны тогда и только тогда, когда равны коэффициенты при одинаковых степенях переменной х, поэтому их следует приравнять.
Пример 2.3.9. Найти 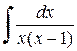 .
.
Решение. По формуле (2.3.2) имеем разложение рациональной дроби  с помощью неопределенных коэффициентов А и В на простейшие дроби:
с помощью неопределенных коэффициентов А и В на простейшие дроби:
 .
.
Откуда с учетом замечания 2.3.1 имеем  . следовательно
. следовательно
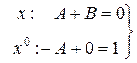

Значит разложение данной рациональной дроби таково 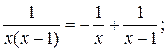 тогда
тогда
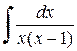
 .
.
Пример 2.3.10. Найти 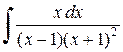 .
.
Решение. По формуле (2.3.2) имеем разложение рациональной дроби  с помощью неопределенных коэффициентов А,
с помощью неопределенных коэффициентов А, 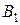 и
и  на простейшие дроби:
на простейшие дроби:
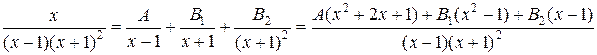 .
.
Откуда с учетом замечания 2.3.1 имеем 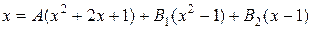 . следовательно
. следовательно
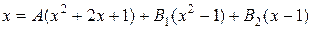
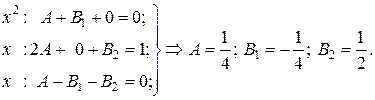
Тогда 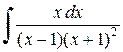
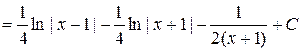 .
.
2 вид
Замечание 2.3.2. Если многочлен 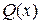 имеет комплексные корни:
имеет комплексные корни:  , кратности k, то в разложение (2.3.2.) войдут простейшие дроби вида:
, кратности k, то в разложение (2.3.2.) войдут простейшие дроби вида: 
Пример 2.3.11. Вычислить  .
.
Решение. Поскольку корни знаменателя рациональной дроби в данном интеграле комплексные 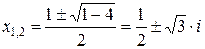 , с учетом замечания 2.3.2 по формуле (2.3.2) имеем разложение рациональной дроби
, с учетом замечания 2.3.2 по формуле (2.3.2) имеем разложение рациональной дроби  с помощью неопределенных коэффициентов А,
с помощью неопределенных коэффициентов А,  и
и  на простейшие дроби:
на простейшие дроби:
 ,
,
Откуда с учетом замечания 2.3.1 имеем 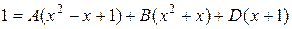 . следовательно
. следовательно
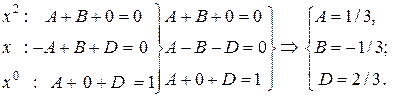
Тогда


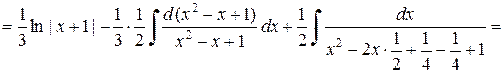

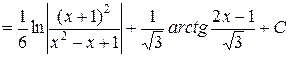 .
.
Пример 2.3.12. Найти  .
.
Решение. Подынтегральная функция является неправильной рациональной дробью:  .
.
Выделим целую часть, разделив числитель на знаменатель по правилу деления многочленов:
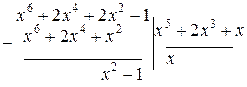
Т.о. подынтегральную функцию можно представить в виде суммы целой части и неправильной рациональной дроби: 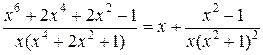 , тогда
, тогда 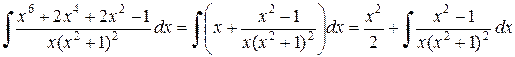 .
.
По формуле (2.3.2) имеем: 
 =
= 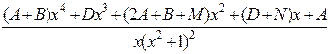 .
.
По замечанию 2.3.1 имеем:
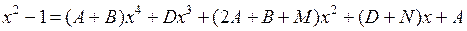 , следовательно
, следовательно
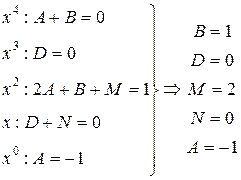
Тогда 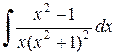 =
= 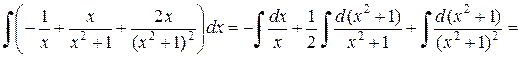
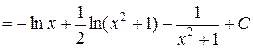 или окончательно получим:
или окончательно получим:

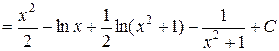 .
.
Дата добавления: 2015-10-30; просмотров: 112 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Интегрирование с помощью замены переменной | | | Интегрирование тригонометрических функций |