Метод подведения под знак дифференциала

Пусть подынтегральная функция может быть представлена в виде

.

Применим формулу (3.1) справа налево. При этом заменим функцию за новую переменную (). Тогда получим . В результате получим следующую схему вычисления интеграла:

, (3.2)

где полученный интеграл справа вычисляется проще, чем исходный интеграл, или вообще сводится к одному из табличных интегралов. После его вычисления необходимо вернуться к переменной , учитывая .

Заметим, что при этом способе не требуется выражать через . Свое название этот метод получил потому, что в процессе преобразования

функция подводится под знак дифференциала. Причем, при достаточном опыте применения этого метода функцию воспринимают как единую переменную мысленно и на бумаге ее уже не заменяют переменной .

Пример 2. Вычислить .

Решение. Замечая, что , применим формулу (3.2):

,

или же, обозначая буквой только мысленно, получаем то же самое:

.

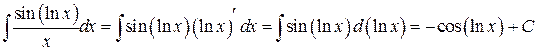Пример 3. Вычислить , .

Решение. Замечая, что , применим формулу (3.2):

,

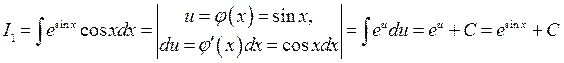или же, обозначая 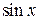буквой только мысленно, получаем то же самое:

.

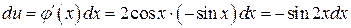Во втором интеграле замечаем, что если обозначить , то . Применяя формулу (3.2), получим

.

Формула (3.2) успешно применяется и в том случае, если для представления подынтегральной функции в форме не хватает всего лишь постоянного множителя, на который подынтегральную функцию следует умножить, а интеграл – разделить на такое же число.

Пример 4. Вычислить , .

Решение. Замечаем, что , т.е. в подынтегральном выражении не хватает множителя 1/2. В связи с этим в прямых скобках сделаем дополнительные преобразования:

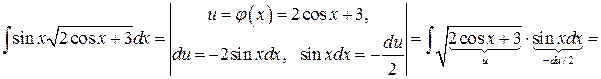
Пример 5. Вычислить , , .

Решение. Для вычисления первого интеграла примем , так как , :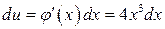

.

Для вычисления второго интеграла примем , так как , :

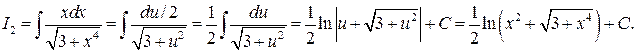
Для вычисления третьего интеграла примем , так как :

При вычислении некоторых интегралов приходится несколько раз применять метод замены переменной.

Пример 6. Вычислить .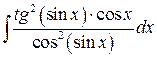

Решение. Для вычисления интеграла примем сначала , тогда . Получаем по формуле (2.2):

.

К полученному интегралу теперь применим замену 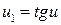, так как . В результате

Лекция 3

Дата добавления: 2015-10-30