Метод непосредственного интегрирования функций

ЛЕКЦИИ ПО ДИСЦИПЛИНЕ

«Математический анализ»

для направления 080100 «Экономика»

Рязань 2012

Тема 5. Неопределенный интеграл функции одной переменной

Лекция 1

Понятие неопределенного интеграла функции одной переменной.

Свойства неопределенного интеграла

Ставится задача: найти для функции 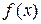такую функцию 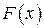, что ее производная равна 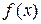(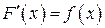). Такую задачу назовем задачей интегрирования функции .

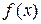Определение 1.1. Функция 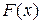называется первообразной для функции 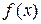на интервале , если при всех .

Например, для функции 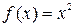имеем первообразную 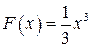, а также 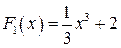, , 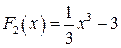причем .

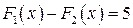Теорема 1.1.

1). Если 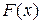– первообразная для функции 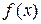, то функция 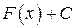(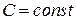) также первообразная для функции .

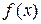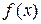2). Если – первообразные для функции , то ().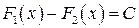

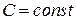Определение 1.2. Пусть 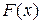– первообразная для функции 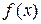на интервале . Множество всех первообразных вида 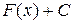(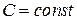) называется неопределенным интегралом от функции 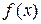и обозначается

. (1.1)

Функцию 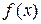называют подынтегральной функцией, выражение 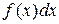подынтегральным выражением, символ 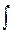– операцией интегрирования (знаком интеграла). Задача нахождения неопределенного интеграла (1.1) называется задачей интегрирования функции. Для нахождения неопределенного интеграла (1.1) для функции 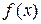достаточно найти хотя бы одну первообразную 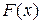и прибавить константу 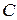. Итак, из приведенного выше запомним, что

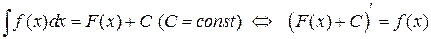. (1.2)

Приведем простейшие и важные для практического применения свойства неопределенных интегралов.

Теорема 1.2 (Свойства неопределенных интегралов). Пусть 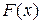–первообразная для функции 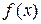на интервале . Тогда

1) ;

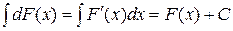2) ;

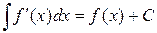3) ;

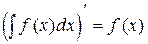4) постоянный множитель можно выносить из-под знака интеграла:

;

5) неопределенный интеграл от суммы функций равен сумме неопределенных интегралов: ;

6) если 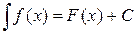, то , 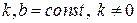(интеграл с измененным линейным аргументом).

Доказательство. Свойства 1) – 5) доказываются просто на основании производных. Аналогично доказывается и свойство 6). Покажем на основании формулы (1.2), что :

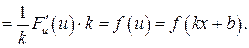
Таблица неопределенных интегралов.

Метод непосредственного интегрирования функций

Приведем таблицу основных (элементарных) неопределенных интегралов.

№	Интеграл	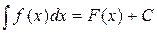№	Интеграл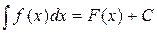
T1		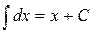T2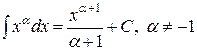
T3		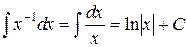T4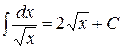
T5		T6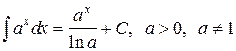
T7		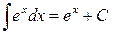T8
T9		T10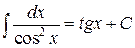
T11		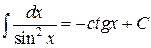T12
T13		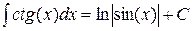T14
T15		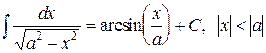T16
T17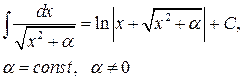

Для доказательства табличных интегралов используем равенство (1.2). Чтобы проверить справедливость табличного интеграла достаточно продифференцировать правую часть и показать, что найденная производная совпадает с подынтегральной функцией .

Рассмотрим, например, табличный интеграл Т14. Пусть ,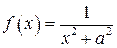

. Очевидно, что

.

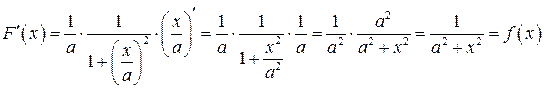Рекомендуем проверить справедливость остальных табличных интегралов (в особенности в Т15 – Т17). После вычисления неопределенного интеграла советуем делать проверку путем дифференцирования (использовать равенство (1.2)). На свойствах неопределенного интеграла и таблицы интегралов основан метод непосредственного интегрирования (метод подведения под табличные интегралы).

Пример 1. Вычислить .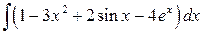

Решение. Используем сначала свойства 4), 5), а затем табличные интегралы (подписываем под интегралом соответствующий номер в таблице):

().

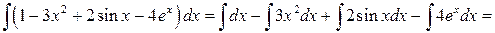
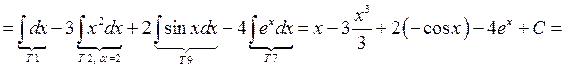
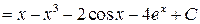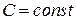Пример 2. Вычислить .

Решение. Учитывая, что 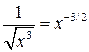, , 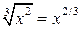получим

.

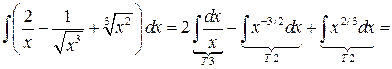
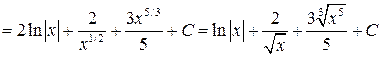Пример 3. Вычислить .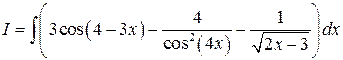

Решение. Имеем .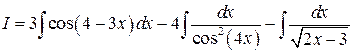

К первому интегралу применяем табличный интеграл и свойство 6), : .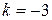

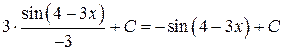Ко второму интегралу применим табличный интеграл 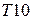и свойство 6), :

.

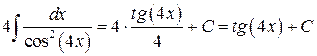К третьему интегралу применим табличный интеграл 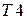и свойство 6), :

.

В результате получим .

Пример 4. Вычислить .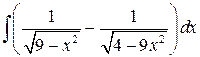

Решение. Имеем .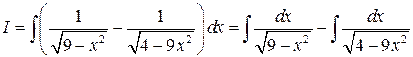

К первому интегралу применим табличный интеграл :

.

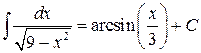Второй интеграл сначала преобразуем, вынеся коэффициент 9 (при ) из-под корня, а затем применим табличный интеграл :

.

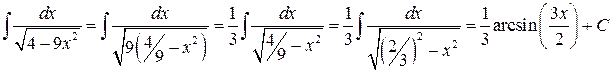В итоге .

Пример 5. Вычислить .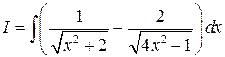

Решение. Имеем 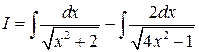. К первому интегралу применим табличный интеграл : .

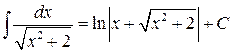Второй интеграл сначала преобразуем, вынеся коэффициент 4 (при )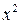

из-под корня, а затем применим табличный интеграл :

.

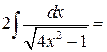
В итоге .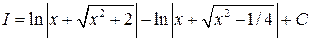

Пример 6. Вычислить .

Решение. Имеем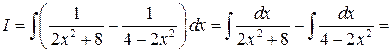

.

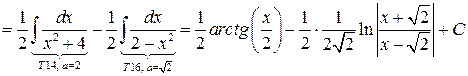Пример 7. Вычислить интеграл .

Решение. Имеем

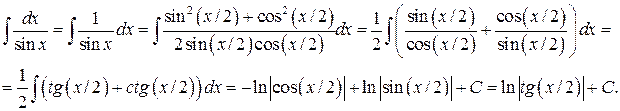
Лекция 2

Дата добавления: 2015-10-30