Свойства определенного интеграла.

1. При перестановке пределов изменяется знак интеграла:

2. Интеграл с одинаковыми пределами равен нулю:

3. Аддитивность. Если отрезок интегрирования разбит на части без общих внутренних точек, то интеграл по всему отрезку равен сумме интегралов по его частям:

4. Линейность.

т.е. интеграл от (алгебраической) суммы функций равен сумме интегралов от каждого слагаемого, а постоянный множитель можно выносить за знак интеграла.

5. Монотонность.

Если для любых 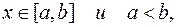то

6. Оценка интеграла.

Если m и M – наименьшее и наибольшее значение функции на отрезке [a; b] и

, то

1. Среднее значение функции:

где

Значение функции в точке c, определяемое из последнего равенства:

называется средним значением функции на отрезке [a; b].

Для вычисления определенного интеграла служит формула Ньютона-Лейбница:

где -какая-нибудь первообразная функции на отрезке [a; b].

При вычислении определенных интегралов используются те же методы и та же таблица основных интегралов, что и при нахождении неопределенных интегралов.

Пусть выполняются следующие условия:

1) функция непрерывна на отрезке [a; b];

2) функция непрерывна вместе со своей производной на отрезке [a; b];

3) ;

4) функция определена и непрерывна на отрезке 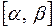, тогда справедлива формула замены переменной (или подстановки)

.

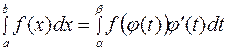Если функции -дифференцируемые на [a; b], то имеет место следующая формула: которая называется формулой интегрирования по частям.

Основные методы интегрирования для определенного интеграла применяются так же, как и для неопределенного. Следует, однако, учесть следующие особенности:

- при замене переменной необходимо изменить пределы интегрирования (тогда не нужно возвращаться к старой переменной, как в неопределенном интеграле), а после нахождения первообразной воспользоваться формулой Ньютона-Лейбница.

- при использовании метода интегрирования по частям необходимо ещё воспользоваться формулой Ньютона- Лейбница.

Дата добавления: 2015-10-30