Приравнивая числители, получим тождество, из которого следует, что

СОДЕРЖАНИЕ

1. Первообразная функция и неопределенный интеграл

2. Таблица простейших интегралов

3. Интегрирование методом замены переменной

4. Метод интегрирования по частям

5. Понятие о неберущихся в конечном виде интегралах

6. Интегрирование рациональных функций

7. Интегрирование тригонометрических рациональных выражений

8. Интегрирование простейших иррациональных выражений

Н Е О П Р Е Д Е Л Ё Н Н Ы Й И Н Т Е Г Р А Л

1. Первообразная функция и неопределенный интеграл

Восстановление функции F (x) по известной производной этой функции F' (x)= f (x) (или по известному ее дифференциалу dF (x)= f (x) dx) называется интегрированием, а искомая функция F (x) называется первообразной функцией.

Всякая функция f (x) имеет бесчисленное множество различных первообразных функций, отличающихся друг от друга на постоянное слагаемое, т.е. если F (x) – первообразная для f (x), то и F (x)+ C, где С - произвольная постоянная, есть также первообразная для f (x), действительно

[ F (x)+ C ]'= F' (x)= f (x). Cовокупность всех первообразных F(x)+C одной и той же функции f(x) называется неопределенным интегралом этой функции и обозначается символом

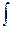
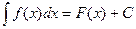, (1)

где x - переменная интегрирования, f(x) - подынтегральная функция, f(x)dx - подынтегральное выражение.

Геометрически, графики всех первообразных функций для f(x) представляют в системе координат XOY семейство кривых, которые получаются одна из другой путем параллельного переноса вдоль оси Y на величину С.

Как следует из понятия неопределенного интеграла, интегрирование и нахождение дифференциала являются обратными действиями. Действительно, если первообразная, а значит и неопределенный интеграл для функции f(x) существует, то подынтегральное выражение представляет собой дифференциал любой из этих первообразных

f(x)dx=F'(x)d(x)=dF(x),

тогда

d∫f(x)dx=d [ F(x)+C ] =F'(x)dx=f(x)dx, (2)

∫dF(x)=∫ f(x)dx=F(x)+C,(3)

т.е. знаки d и ∫ взаимно сокращаются.

Укажем основные свойства неопределенного интеграла, правильность которых можно проверять дифференцированием.

І. Постоянный множитель выносится за знак интеграла.

∫Af(x)dx=A∫ f(x)dx ( 4)

2. Интеграл от алгебраической суммы (разности) функций равен сумме(разности) интегралов.

∫ [ f(x) ± φ(x) ] dx=∫f(x)dx ±∫φ(x)dx. (5)

3. Неопределенный интеграл не зависит от выбора переменной интегрирования.

∫ f(u)du= F(u)+C, (6)

где u - независимая переменная или функция x, u=u(x). Этот результат следует непосредственно из правила дифференцирования сложной функции

; , ,

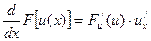тогда

.

4. Интеграл ∫ udv может быть сведен к интегралу ∫ vdu.

Из формулы дифференцирования произведения двух функций d(uv)=udv+vdu

интегрированием получается следующее равенство

∫ udv = uv – ∫vdu, (7)

которое называется формулой интегрирования по частям.

2. Таблица простейших интегралов

Пользуясь тем, что интегрирование – операция обратная вычислению дифференциала можно записать основные формулы интегрирования

1. α ≠ -1

2.

3.

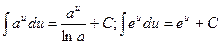
4.

5.

6.

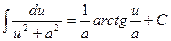
7.

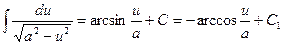
8.

9.

Для полноты таблицы добавим еще две формулы.

10.

11.

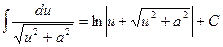
В этих формулах u - независимая переменная или функция от независимой переменной, a – постоянная (в формуле 7 а ).

Приведем простейшие примеры вычисления интегралов:

Пример 1.

Пример 2.

Пример 3.

1.Разлагая интеграл 1 по свойству 2 на три интеграла и вынося постоянный множитель за знак интеграла (свойство 1), приведем интеграл к следующему виду:

далее первый и второй интегралы вычисляются по формуле 1 таблицы, а

в третьем - знаки ∫ и d взаимно сокращаются (интегрирование и взятие дифференциала – обратные действия).

.

2.Интеграл табличный, формула 3.

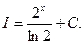
3.Подынтегральная функция (пр.3) может быть преобразована и сведена к разности двух функций, а значит к двум интегралам, интегрируемых по формуле 1 таблицы.

Для вычисления различных интегралов дополним таблицу определенными приёмами и методами интегрирования.

3. Интегрирование методом замены переменной.

Метод замены переменной или подстановки является одним из самых эффективных приемов интегрирования и вытекает из свойства 3.

Пусть требуется вычислить , во многих случаях удается в качестве новой переменной выбрать такую функцию u=u(x), чтобы подынтегральное выражение представилось в виде

,

тогда достаточно найти интеграл

чтобы из него подстановкой u=u(x) получить искомый интеграл, т.е.

(9)

Рассмотрим частный случай замены переменной, если ∫ f(x)dx=F(x)+C, то

(8)

Действительно, , тогда

т.е. и функция оказывается первообразной

для f(ax+b).

Пример 4.

Пример 5. .

Пример 6.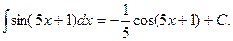

Пример 7.

так как , то полагая , получим

При выборе подстановки , упрощающей подынтегральное выражение, нужно помнить, что в его составе должен найтись множитель , дающий дифференциал новой переменной. В примере 7- это множитель

Приведем ряд примеров на вычисление интегралов, которые заменой переменной сводятся к табличным.

Пример 8.

полагаем тогда и

.

Пример 9.

Замена подставляя новую переменную в исходный интеграл, получим

Пример 10.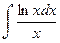

В состав подынтегрального выражения входит множитель , являющийся

дифференциалом функции lnx, отсюда подстановка u=lnx, du=d(lnx) т.е.

Пример 11.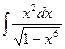

Подстановка x³ = u, du=3x²dx сводит искомый интеграл к другому интегралу, который является табличным.

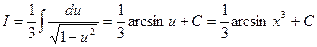ΩΩΩ

Интегрирование дробей, содержащих квадратный трехчлен

(10)

при условии, что квадратный трехчлен x² +px+q не имеет действительных корней .

Для вычисления интеграла из квадратного трехчлена выделяется полный квадрат двучлена т.к. , то подстановка приводит к следующей замене

Искомый интеграл принимает следующий вид:

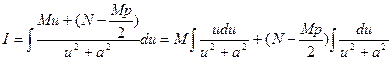
Первый интеграл аналогичен интегралу из примера 8, второй табличный

/формула 6/.

Пример 12.

Выделяем полный квадрат x ² +4 x +10=(x ²+4 x +4)+(10-4), делаем замену x +2= u, тогда 3 x -1=3 u -7, du=dx, подставляем в интеграл

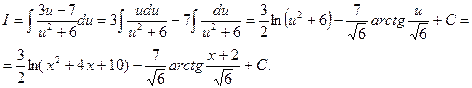
4. Метод интегрирования по частям

Согласно свойству 4 вычисление интеграла может быть сведено к отысканию другого интеграла . Применение формулы целесообразно, если будет проще, чем или подобен ему. Для применения формулы интегрирования по частям к интегралу следует подынтегральное выражение представить в виде произведения двух множителей u и dv. За dv выбирается выражение, которое содержит dx, и из которого v можно получить непосредственным интегрированием, за u, как правило, принимается функция, которая при дифференцировании упрощается, например ln x, arctg x и т.д.

Пример 13.

Примем за , тогда , подставляя в формулу (7), получим

Второй интеграл вычисляется подстановкой , окончательный результат

Пример 14.

Принимаем за , находим 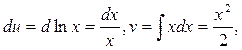подставляем в (7)

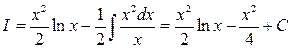
Пример 15.

Пусть , тогда подставляя найденные значения в формулу (7), приходим к следующему интегралу:

Применим метод интегрирования по частям к интегралу полагая

т.е., вычисляя исходный интеграл, мы приходим к подобному в результате исходный интеграл равен:

5. Понятие о неберущихся в конечном виде интегралах.

Для всякой непрерывной в интервале [a,b] функции f(x) существует функция F(x), производная которой в точности равна данной функции. Тем не менее не всегда оказывается возможным интеграл от элементарной функции выразить через элементарные с помощью конечного числа арифметических операций. К числу таких заведомо невыражающихся в «конечном виде» интегралов относятся и ряд других, которые часто называют «неберущимися». Важно подчеркнуть, что все эти интегралы реально существуют, но они лишь представляют собой совершенно новые функции и не приводятся к тем функциям, которые мы называем элементарными.

6. Интегрирование рациональных функций.

Классы функций, интегралы которых выражаются через элементарные с помощью конечного числа арифметических действий, называются интегрируемыми в элементарных функциях. Известны сравнительно немногие классы функций, для которых имеется алгоритмы интегрирования. Простейшим из этих классов является класс рациональных функций R(x).

Напомним, что рациональной дробью называется отношение двух алгебраических многочленов . Рациональная дробь называется правильной, если степень многочлена числителя меньше степени многочлена знаменателя, например дробь

Неправильная дробь может быть представлена в виде целой части, интегрирование которой не представляет труда и остатка в виде правильной дроби. Это можно сделать делением «уголком»

x³-2 x³+x²+x

x ²+x+1

-

-1

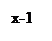
x-1 - целая часть, -1 - остаток

т.е.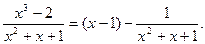

Согласно основной теореме алгебры, многочлен с действительными коэффициентами разлагается, и притом единственным образом, на действительные множители

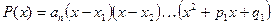(12)

Здесь - действительные корни многочлена, а квадратичные множители не имеют действительных корней и, следовательно, являются неразложимыми на действительные линейные множители. В разложении многочлена некоторые множители могут совпадать и тогда их можно объединить, вводя кратность множителей, например

P (x) = x ³+4 x ²+4 x = x (x ²+4 x +4) = x (x +2)²

В алгебре устанавливается, что каждому множителю вида в разложении знаменателя правильной дроби отвечает группа из k простых дробей:

каждому множителю группа из m простых дробей:

A_i, M _i, N _i - числовые коэффициенты. Таким образом, зная разложение (12) мы знаем знаменатели простых дробей, на которые разлагается заданная дробь:

(13)

Приводя правую часть (13) к общему знаменателю, который очевидно есть P (x), получим дроби, у которых знаменатели равны, а значит равны числители. Неизвестные коэффициенты в разложении (13) находят, приравнивая коэффициенты при различных степенях х многочлена Q (x) к соответствующим коэффициентам справа, – такой метод называют методом неопределенных коэффициентов. Итак, любую рациональную дробь можно разложить на простые дроби, которые интегрируются в конечном виде.

Пример 16.

Преобразуем подынтегральную функцию

Приравнивая числители, получим тождество, из которого следует, что

коэффициенты при одинаковых степенях х слева и справа равны

при x ³ справа A ₁+ M= 0, при x ² A ₂+ N = 2, при x ¹ 3 A ₁ = -1, при x ⁰ 3 A ₂= 1

откуда

Подынтегральная функция примет вид: .

Искомый интеграл запишется в виде суммы трёх интегралов

.

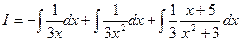Первые два интеграла – табличные, третий вычисляется разложением на два интеграла, один из которых также табличный, а другой заменой переменной сводится к табличному. Окончательный результат:

Пример 17.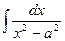

Интеграл вычисляется разложением подынтегральной функции на простые дроби, используя метод неопределенных коэффициентов

Сравнивая числители слева и справа, получим A ₁+ A ₂=0, A ₁- A ₂=1/ a, тогда A ₁= 1/2 a, A ₂ = – 1/2a, подставляя в искомый интеграл, получим

*

Итак, интеграл от любой рациональной дроби выражается через элементарные функции. Кроме рациональных дробей в элементарных функциях интегрируются также и ряд других классов функций. Как правило, интегралы от таких функций сводятся подстановкой к интегралу от рациональной дроби, т.е. подстановка рационализирует интеграл от рассматриваемой функции.

6. Интегрирование тригонометрических рациональных выражений.

Интегралы типа в общем случае рационализируются

тригонометрической подстановкой . В новых переменных

____________________________________________

Формула 10 таблицы (стр. 5).

Пример 18.

Пользуясь заменой , вместо исходного, получим следующий интеграл

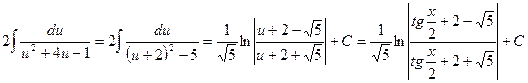
Частные случаи вычисления интегралов, содержащих тригонометрические функции.

a) Интегралы вида: , где хотя бы одно из чисел n или m нечетные числа, вычисляются заменой переменной путем отделения одного множителя.

Пример 19.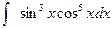

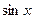
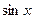
Выделяется множитель , который является дифференциалом , =- . Отсюда подстановка и интеграл сводится к следующему виду:

б) Интегралы вида: где n и m - четные числа вычисляются путем понижения степени вдвое по тригонометрическим формулам

Пример 20.

в) Интегралы , ,

вычисляются также с помощью тригонометрических формул:

,

,

,

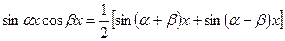которые приводят их к табличным.

Пример21.

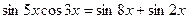, интеграл принимает вид:

8.Интегрирование простейших иррациональных выражений.

Интегрирование линейных иррациональностей.

Интеграл от рациональной функции рационализируется

подстановкой , где n - общий знаменатель всех дробных показателей выражений ax+b, тогда ax+b=u ⁿи dx=n/a∙ u^n-1du

Пример 22.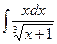

Положив , получим x +1 = u ³, x = u³ -1, dx =3 u² du, интеграл примет вид:

Возвращаясь к переменной х, имеем

Интегрирование простейшей квадратичной иррациональности

В этом интеграле >0. Представим подынтегральную функцию в следующем виде

тогда интеграл можно разложить на сумму двух интегралов

.

Первый вычисляется подстановкой u = , du = dx

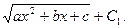
Второй интеграл

следует рассмотреть отдельно, предполагая конечно, что квадратный трехчлен не имеет равных корней, так что корень из него не может быть заменен рациональным выражением. С помощью дополнения квадратного трехчлена до полного квадрата (см. § 4) этот интеграл, в зависимости от вида квадратного трехчлена, сводится к одному из следующих интегралов:

.

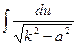Третий интеграл табличный (формула 7), первые два вычисляются так называемой подстановкой Эйлера. Подстановка Эйлера для первого интеграла приводит к следующей формуле:

*

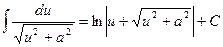
Пример 23.

Вторая подстановка Эйлера применима к интегралам второго типа, т.е. когда квадратный трехчлен имеет действительные корни и приводит к формуле:

Пример 24.

.

В общем случае, интегрирование выражений вида 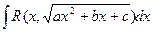проводится по методу рационализации подынтегральной функции с помощью подстановок Эйлера.

_____________________________

*Формула 11 таблицы интегралов.

Дата добавления: 2015-10-30