Замена переменной в определенном интеграле

Пусть:

1. функция 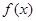определена и непрерывна на отрезке ;

2. функция определена и непрерывна вместе с производной на отрезк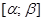е , где .

Тогда .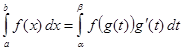

Замена переменной в определенном интеграле требует осторожности и обязательного выполнения всех перечисленных условий, налагаемых на функцию . При соблюдении этих требований важно отметить, что замена переменной в определенном интеграле приводит в общем случае к интегралу с новыми пределами интегрирования.

Эти пределы находятся так:

Ø в функцию подставляется сначала нижний предел заданного интервала и решается уравнение . Значение , найденное из него, и будет новым нижним пределом . Если этому уравнению удовлетворяет не одно, а несколько значений , то за значение можно принять любое из них.

Ø Затем для определения нового предела в функцию подставляется верхний предел заданного интеграла и решается уравнение . Найденное из этого уравнения значение будет новым верхним пределом 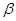. Если это уравнение имеет несколько корней, то за значение 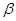можно принять любое из них.

Ø Однако свобода выбора чисел ограничивается требованием, чтобы значения функции 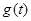не выходили из отрезка 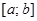, в котором определена и непрерывна подынтегральная функция .

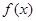Сделав замену переменной, изменив пределы интегрирования, после вычисления преобразованного определенного интеграла нет необходимости переходить к старой переменной, как это мы делали при вычислении неопределенного интеграла с помощью замены переменной.

Во многих случаях приходится вместо подстановки , которая переменную интегрирования заменяет функцией новой переменной, вводить новую переменную как функцию старой переменной , т. е. полагать

.

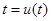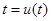В этом случае новые пределы интегрирования . Если соотношение разрешить относительно , то окажется, что , причем необходимо, чтобы для функции 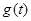были соблюдены все указанные выше условия.

Итак, замена переменной в определенном интеграле осуществляется по тем же правилам, что и в неопределенном интеграле, только нет обратного перехода к исходной переменной и есть новая операция – замена пределов интегрирования (новые пределы интегрирования вычисляются по старым через замену).

Задача 5.3. Вычислить интегралы: 1) ; 2) ; 3) ; 4) .

1) ▲

. ▼

2) ▲

. ▼

3) ▲

. ▼

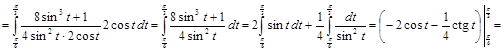
4) ▲

. ▼

Решение задач I типового варианта

Вычислить определенные интегралы с точностью до двух знаков после запятой.

1. ▲

. ▼

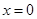
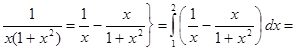
2. ▲

. ▼

3. ▲

,

,

,

. ▼

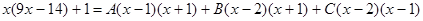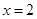
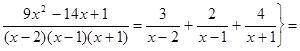
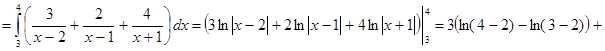
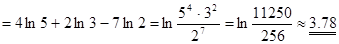4. ▲

. ▼

5. ▲

. ▼

6. ▲

. ▼

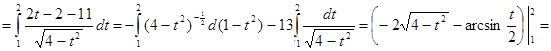
7. ▲

. ▼

Дата добавления: 2015-10-30