Вычисление объемов тел вращения. Телом будем называть любое ограниченное множество точек пространства.

Телом будем называть любое ограниченное множество точек пространства.

Тело вращения – тело, полученное в результате вращения фигуры вокруг некоторой оси (оси вращения).

Объем тела вращения – аддитивная величина, следовательно, объем тела вращения можно определить с помощью определенного интеграла.

Вычисление объема в прямоугольной системе координат. Воспользуемся дифференциальным методом.

1. Найти дифференциал объема как главную часть приращения объема.

2. Определить пределы интегрирования .

3. Вычислить объем .

Дифференциал объема в прямоугольной системе координат – объем цилиндра с бесконечно малой высотой и переменным основанием.

Форма записи дифференциала объема зависит от условий задачи – от того, как задана фигура, которая в результате вращения образует тело, и что принято за ось вращения.

Ось вращения будем отмечать дугой со стрелкой

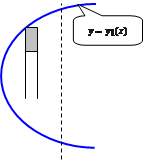
2. y

1. y

y

O a x a=0 dx b x

dx

. .

4. y

3. y

d

d

dy

dy

c

O x c=0 x

. .

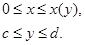
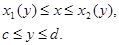
Замечание. На всех чертежах изображено сечение тела плоскостью чертежа.

Задача 7.2.1. Фигура, ограниченная линиями , вращается вокруг оси . Найти объем тела вращения.

▲ – полукубическая парабола, смещенная на 1 вправо по оси . – прямая.

Точки пересечения полукубической параболы и прямой:

. Построение очевидно.

y

B

O 1 2 x

dx

1) Имеем дифференциал объема: .

2) Пределы по чертежу: .

3) Вычислим объем: . ▼

Задача 7.2.2. Фигура, ограниченная линиями , вращается вокруг оси .

Найти объем тела вращения.

▲ – парабола, – прямая. Точки пересечения параболы и прямой:

. Построим чертеж:

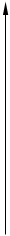y

A

O 4 x

1) Найдем .

2) Пределы определяем из решения системы при определении точек пересечения параболы и прямой: .

3) Вычисляем объем:

. ▼

Вычисление объема при параметрическом задании линий, ограничивающих фигуру.

Задача 7.2.3. Фигура, ограниченная одной аркой циклоиды и осью вращается вокруг оси . Найти объем тела вращения.

▲ Чертеж циклоиды очевиден.

y

Odx 2π a x

1) .

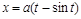2) Пределы определяются по пределам из зависимости . Имеем

3)

.

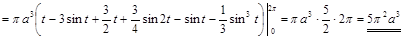Вычисление длин плоских кривых при различных способах задания линий

Дата добавления: 2015-10-30