Основные понятия и формулы

1. Длина кривой.

Рассмотрим на плоскости кривую , заданную параметрически:

,

где – непрерывные функции на отрезке , причем различным значениям соответствуют различные точки (т. е. нет кратных точек). Такую кривую назовем простой (плоской) незамкнутой кривой.

Если точки совпадают, а остальные точки не являются кратными, то кривая называется простой замкнутой кривой.

Длина дуги – аддитивная величина, следовательно, ее можно найти с помощью определенного интеграла.

Воспользуемся дифференциальным методом.

1. Найти дифференциал дуги в зависимости от способа задания кривой.

2. Определить пределы интегрирования.

3. Вычислить интеграл от дифференциала дуги.

2. Длина кривой в декартовых координатах. Если кривая задана уравнением

,

причем функция имеет на отрезке 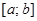непрерывную производную, то дифференциал дуги вычисляется по формуле

,

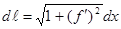а длина кривой по формуле

.

Если кривая задана уравнением

,

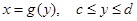причем функция имеет на отрезке 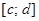непрерывную производную, то дифференциал дуги вычисляется по формуле

,

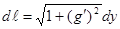а длина кривой по формуле

.

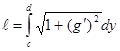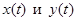3. Длина кривой, заданной параметрически. Пусть кривая задана параметрическими уравнениями , причем функции имеют на отрезке непрерывные производные. Тогда дифференциал дуги выражается формулой

а длина кривой

.

4. Длина кривой в полярных координатах. Если кривая задана уравнением 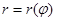, , причем функция имеет на отрезке непрерывную производную, дифференциал дуги выражается формулой

,

а длина кривой

.

Замечание. Задачи на вычисление длин дуг можно решать без чертежа.

Задача 7.3.1. Найти длину дуги кривой .

▲ 1.

.

2. Пределы заданы в условии задачи .

3.

. ▼

Задача 7.3.2. Вычислить длину дуги одной арки циклоиды .

▲ Кривая задана параметрически.

1.

.

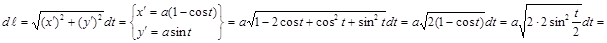
2. Пределы для переменной определяются по пределам из уравнения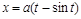

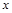
3. . ▼

Задача 7.3.3. Вычислить длину логарифмической спирали .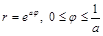

▲ Кривая задана в полярной системе координат.

1. .

2. Пределы заданы по условию задачи: .

3. .

Решение задачи III типового варианта

Вычислить (с точностью до двух знаков после запятой) площадь фигуры, ограниченной указанными линиями .

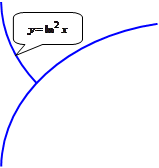
▲ Найдем точки пересечения данных кривых:

.

Сделаем чертеж.

y

1 B

A

O 1 dx e x

1. Имеем: .

2. Пусть область правильная относительно оси :

3.

. ▼

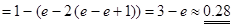Решение задачи IV типового варианта

Вычислить (с точностью до двух знаков после запятой) объем тела, полученного вращением вокруг оси абсцисс плоской фигуры, ограниченной параболами .

▲ – парабола, строится по трем точкам:

Вершина определяется из условия .

.

Точки пересечения с осью .

.

– парабола. Вершина определяется из условия .

.

Точек пересечения с осью нет .

Находим точки пересечения данных парабол:

.

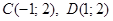y

A

C D

B

dx x

1. Дифференциал объема:

.

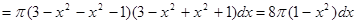2. Пределы определяем из решения системы (пересечения парабол): .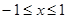

3. . ▼

Дата добавления: 2015-10-30