
Читайте также:
|
Плоской фигурой будем называть любое ограниченное множество точек плоскости.
Так как площадь – аддитивная величина, то ее можно вычислить с помощью определенного интеграла.
Воспользуемся дифференциальным методом.
1. Найти дифференциал площади 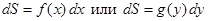 .
.
2. Определить пределы интегрирования 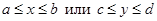 .
.
3. Вычислить площадь 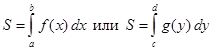 .
.
Перед решением задачи на вычисление площадей необходим чертеж, для построения которого нужно исследовать поведение функции или воспользоваться тем, что вид графика известен, и построить линию по нескольким точка
Вычисление площади в прямоугольной системе координат. Дифференциал площади в прямоугольной системе координат – площадь прямоугольника с бесконечно малым основанием и переменной высотой. Форма записи дифференциала зависит от способа задания фигуры, от условий задачи.
Пусть 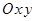 – прямоугольная декартова система координат. Фигуры будем задавать с помощью неравенств или систем неравенств.
– прямоугольная декартова система координат. Фигуры будем задавать с помощью неравенств или систем неравенств.
Определение. Область называется правильной (стандартной) относительно оси 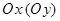 , если любая горизонтальная (вертикальная) прямая пересекает границу области не более чем в двух точках.
, если любая горизонтальная (вертикальная) прямая пересекает границу области не более чем в двух точках.
Если область правильная относительно осей 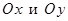 , то она просто называется правильной областью.
, то она просто называется правильной областью.
 Условимся дальше области, правильные относительно оси
Условимся дальше области, правильные относительно оси 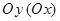 , штриховать линиями, параллельными оси
, штриховать линиями, параллельными оси 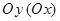 .
.
y
 |
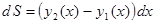
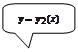

O a dx b x

Область правильная относительно оси 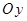 .
.
Если область 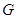 , правильная относительно оси
, правильная относительно оси 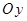 , проектируется на ось
, проектируется на ось 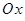 в отрезок
в отрезок 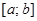 , то ее граница разбивается на две линии: нижнюю границу области, задаваемую уравнением
, то ее граница разбивается на две линии: нижнюю границу области, задаваемую уравнением 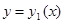 и верхнюю, задаваемую уравнением
и верхнюю, задаваемую уравнением 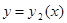 .
.
Тогда область 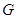 определяется системой неравенств
определяется системой неравенств
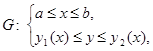
а площадь 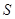 вычисляется по формуле
вычисляется по формуле
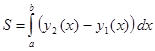 .
.
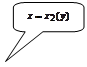
 y
y




 d
d
 |  |  | ||||||
 |  |  |





 dy
dy 



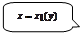
 |  | ||||
 |
 c
c
 |
O x
Область правильная относительно оси 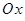 .
.
Если область 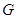 , правильная относительно оси
, правильная относительно оси 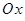 , проектируется на ось
, проектируется на ось 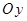 в отрезок
в отрезок 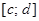 , то ее граница разбивается на две линии: левую границу области, задаваемую уравнением
, то ее граница разбивается на две линии: левую границу области, задаваемую уравнением 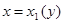 и правую, задаваемую уравнением
и правую, задаваемую уравнением  . В этом случае область
. В этом случае область 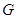 определяется системой неравенств
определяется системой неравенств
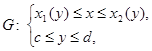
а площадь 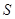 вычисляется по формуле
вычисляется по формуле
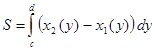 .
.
Задача 7.1.1. Найти площадь фигуры, ограниченной линиями 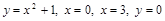 .
.
▲ 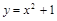 – парабола;
– парабола; 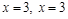 – прямые линии.
– прямые линии.
Найдем точки пересечения данных линий:
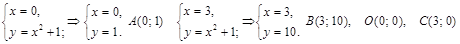
Построение очевидно.
 |
 y
y
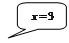 B
B
 |
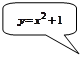

 A
A


O dx C x
Найдем 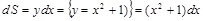 .
.
Область 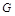 , правильная относительно оси
, правильная относительно оси  , определяется системой неравенств
, определяется системой неравенств
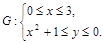
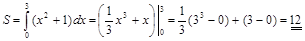 . ▼
. ▼
Замечание. Единицы измерения площадей всюду опускаются (для простоты).
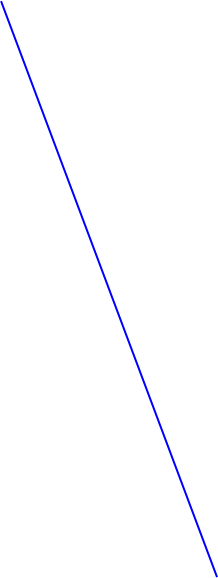
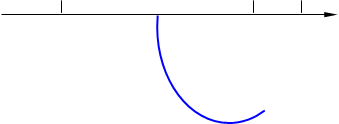
Задача 7.1.2. Найти площадь фигуры, ограниченной линиями 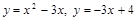 .
.
▲ 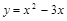 – парабола, которая строится по трем точкам: вершина определяется из условия
– парабола, которая строится по трем точкам: вершина определяется из условия 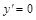 .
.
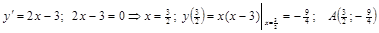 .
.
Точки пересечения с осью 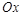 :
:  .
.
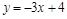 – прямая, которая строится по двум точкам, в качестве которых возьмем точки пересечения данных линий:
– прямая, которая строится по двум точкам, в качестве которых возьмем точки пересечения данных линий: 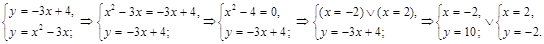
 .
.
 |
y


 C 10
C 10
 | |
 | |
 | |
 | |
 |
 4
4
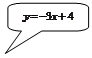 | |||||||||
 | |||||||||
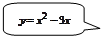 | |||||||||
 |  | ||||||||
 | |||||||||
 |

–2 O dx 2 B x

 A D
A D
1) Имеем: 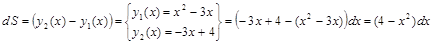 .
.
2) Область 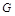 , правильная относительно оси
, правильная относительно оси  , определяется системой неравенств
, определяется системой неравенств
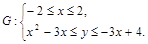
3) 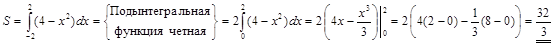 . ▼
. ▼
Задача 7.1.3. Найти площадь фигуры, ограниченную параболой 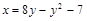 и осью
и осью  .
.
▲ 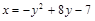 – парабола, которая строится по трем точкам: вершина определяется из условия
– парабола, которая строится по трем точкам: вершина определяется из условия 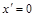 .
.
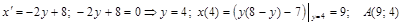
Точки пересечения с осью  :
:
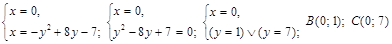 .
.
 |
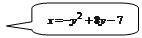 y
y

 C
C

 A
A
dy

 B
B
O x
1) Найдем 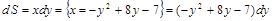 .
.
2) Область 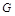 , правильная относительно оси
, правильная относительно оси 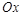 , определяется системой неравенств
, определяется системой неравенств
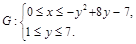
3) 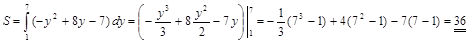 . ▼
. ▼
Задача 7.1.4. Найти площадь фигуры, ограниченной линиями 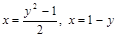 .
.
▲ 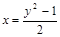 – парабола, которая строится по трем точкам: вершина определяется из условия
– парабола, которая строится по трем точкам: вершина определяется из условия 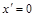 .
.
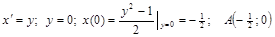 .
.
Точки пересечения с осью  :
:
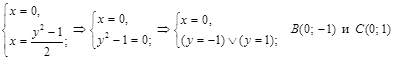 .
.
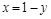 – прямая, которая строится по двум точкам, в качестве которых возьмем точки пересечения данных линий:
– прямая, которая строится по двум точкам, в качестве которых возьмем точки пересечения данных линий:
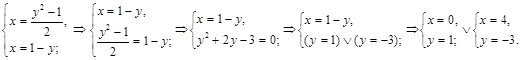
 .
.

y
 |
C

 A
A
 O B 4 x
O B 4 x


 dy
dy
 –3 D
–3 D
1) Имеем 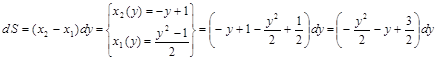 .
.
2) Область 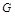 , правильная относительно оси
, правильная относительно оси  , определяется системой неравенств
, определяется системой неравенств
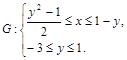
3) 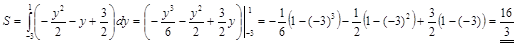 . ▼
. ▼
Вычисление площадей при параметрическом задании линий, ограничивающих фигуру. В задачах такого типа последовательность действий сохраняется, чаще всего усложняется отыскание пределов.
Пусть граница плоской области фигуры 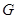 – простая замкнутая кривая, заданная параметрически уравнениями
– простая замкнутая кривая, заданная параметрически уравнениями 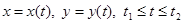 , причем точка
, причем точка 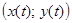 при изменении
при изменении 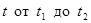 границу области
границу области 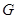 так, что фигура
так, что фигура 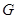 остается слева от движущейся точки. Тогда площадь фигуры
остается слева от движущейся точки. Тогда площадь фигуры 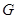 может быть вычислена по любой из следующих формул:
может быть вычислена по любой из следующих формул:
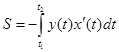 ,
,
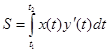 ,
,
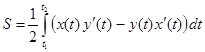 .
.
Задача 7.1.5. Найти площадь эллипса: 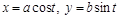 .
.
▲ Чертеж очевиден.
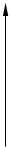 y
y


 b
b
 |
O dx a x
1) Имеем 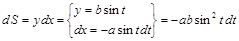 .
.
2) С учетом свойств симметрии фигуры при определении 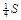 пределы находим по изменению
пределы находим по изменению 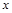
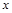
| 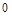
| 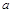
|

| 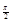
|
3) 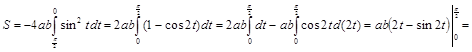
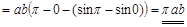 . ▼
. ▼
Вычисление площадей в полярной системе координат. Вычисление площадей в полярной системе координат производится по дифференциальному методу без каких-либо изменений в его операциях и их последовательности.
Дифференциалом площади в полярной системе координат является площадь кругового сектора с бесконечно малым центральным углом 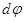 и переменным радиусом
и переменным радиусом 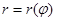 :
:
 .
.
Форма записи дифференциала площади зависит от способа задания фигуры в полярной системе координат.
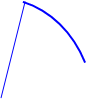
 I.
I. 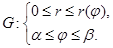 II.
II. 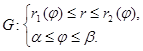
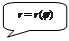 | |||||
 | |||||
 | |||||

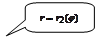


 dφ dφ
dφ dφ
 | |||
 |



 β β
β β
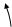
 α α
α α


O p O p
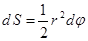
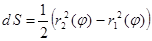
Задача 7.1.6. Найти площадь фигуры, ограниченной лемнискатой Бернулли 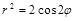 .
.
▲ Напоминаем, что в полярной системе координат чертеж строится по точкам.
Сначала выясняется, где расположена линия по признаку 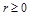 :
:
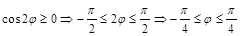 .
.
Затем по периодичности косинуса находим количество петель. Здесь их 2.
Находится 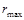 по условию
по условию 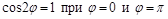 .
.
Построение графика очевидно.
 |
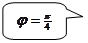







 O 2 p
O 2 p
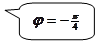 |
Далее все операции совпадают с действиями, рассмотренными раньше.
1) 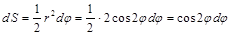 .
.
2) Пределы по условию существования функции 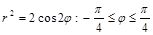 .
.
Или с учетом свойств симметрии фигуры при определении 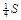 пределы находим:
пределы находим: 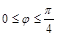 .
.
3) 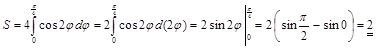
Замечание. Кривые вида 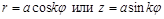 называются розами. Розы имеют
называются розами. Розы имеют 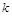 лепестков (петель), если
лепестков (петель), если 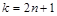 , и
, и 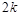 петель, если
петель, если 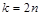 .
.
Например, 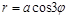 – трехлепестковая роза,
– трехлепестковая роза, 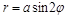 – четырехлепестковая роза.
– четырехлепестковая роза.
При вычислении площадей, ограниченных розами, достаточно найти площадь одного лепестка и затем ее умножить на число лепестков.
Дата добавления: 2015-10-30; просмотров: 280 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Вычисление несобственных интегралов | | | Вычисление объемов тел вращения |