Углубленное Рассуждение

Раасмотрим пристальнее влияние изменения веса выбранной контр. точки. Давайте вернемся к определению кривой NURBS:

Выберем контр. точку p_k и исследуем влияние изменения w_k. Так как p_k может влиять на кривую p(u) только на ненулевой области ее коэффициента N_k,p(u) (т.e. [u_k, u_k+p+1)), то далее примем, что u лежит на [u_k, u_k+p+1).

Вынесем члены с w_k из суммирования, получим:

Так как это уравнение довольно сложное, упростим его следующим способом:

Теперь уравнение стало таким легкочитаемым:

Сначала возьмем случай w_k = 0. Имеем A = 0, и точка на кривой, обозначается как p⁰(u), равна

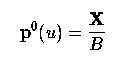
Теперь давайте вычислим вектор из этой "базисной" точки p⁰(u) в соответствующую ей точку p(u) для произвольного w_k. После простых преобразований имеем следующее:

Что это значит? Это значит, что вектор p(u)-p⁰(u) и вектор p_k-p⁰(u) имеют одно направление, а длина первого в A/(A+B) больше, чем длина последнего для каждого u на [u_k, u_k+p+1)! Так как точки p_k и p⁰(u) фиксированы, то можно сказать, что p(u) лежит на прямой от p_k до p⁰(u). Более того, если все весы неотрицательны, то и A, и B неотрицательны и значение A/(A+B) лежит между 0 и 1! То есть, точка p(u) лежит на отрезке между p_k и p⁰(u).

Что, если w_k достигает бесконечности? Давайте поделим числитель и знаменателm кривой p(u) на w_k, как показано ниже.

Если w_k уходит в бесконечность, 1/w_k становится нулем. Отсюда, если w_k достигает бесконечности, то p(u) достигает p_k, выбранной контр. точки. Вот итог сказанного:

Если w_k неотрицательно, то p(u) всегда лежит на отрезке между p⁰(u) и p_k, где p⁰(u) - это точка, соответствующая w_k = 0, а u лежит на [u_k, u_k+p+1). Более того, когда w_k изменяется от 0 до бесконечности, p(u) двигается от p⁰(u) к p_k, а если w_k - бесконечность, то p(u) становится p_k.

Следующий рисунок иллюстрирует этот результат. Имеем кривую NURBS 6 степени, определенную по 9 контр. точкам (n = 8) и 16 узлам (m = 15), как показано ниже.

u0 = u1 = u2 = u3 = u4 = u5 = u6	u7	u8	u9 = u10 = u11 = u12 = u13 = u14 = u15
	1/3	2/3

Выбранная контр. точка - это p₄. Так как коэффициент при p₄, N_4,6(u), не рваен нулю на [u₄, u₄₊₆₊₁) = [0,1), то изменение w₄ влияет на кривую целиком!

Точки, соответствующие u = 1/3 и u = 2/3 обозначены на кривой разными цветами. Кривая, соответствующая w₄ = 0 - самая нижняя, обозначена 0. Риснуок показывает кривые для w₄, равного 2, 3, 4, 5, 10, 20 и 50. При увеличении значения w₄ кривая пододвигается ближе к контр. точке p₄. Когда w₄ увеличивается до 50, кривая становится очень близко к p₄. Пожалуйста, заметьте, что все точки, соовтетствующие p(1/3) находятся на отрезке прямой между точками p⁰(1/3) и p₄, а все точки, соответствующие p(2/3) - на отрезке прямой между p⁰(2/3) и p₄. Также заметьте, что отрезок кривой между точками p(1/3) и p(2/3) становится короче при увеличении значения w₄. В конце концов длина этого криволинейного отрезка становится равной нулю (т.e. p(1/3) и p(2/3) становится равно p₄), когда w₄ равно бесконечности. Можете ли вы обобщить это наблюдение?

Дата добавления: 2015-10-29