Глобальная Аппроксимация Кривых

В интерполяции, интерполированная кривая проходит через все данные исходные точки в данном порядке. Как обсуждалось в Глобальной Интерполяции, интерполированная кривая может вилять между исходными точками, а не следовать форме исходной ломаной. Метод аппроксимации вводится для того, чтобы избежать этой проблемы при помощи ослабления строгого требования того, что кривая должна содержать все исходные точки. Кроме первой и последней точек, кривая не обязана содержать никаких других. Чтобы измерить, насколько хорошо кривая "аппроксимируется" к исходной ломаной, вводится понятие расстояния погрешности. Расстояние погрешности - это расстояние между исходной точкой и "соответствующей" ей точке на кривой. Таким образом, если минимизировать расстояния погрешности, то кривая будет проходить близко к исходной ломаной. Интерполированная кривая - это как раз такое решение, потому что для нее расстояние погрешности каждой исходной точки равно нулю. Тем не менее, здесь пойдет обсуждение не об интерполяции кривых. Кривая, полученная таким способом, называется аппроксимированной.

Пусть дано n +1 исходных точек d ₀, d ₂,..., d _n, и нам нужно найти кривую B-spline, которая бы следовала форме этой ломаной, но не обязательно проходила через них. Чтобы это сделать, нам нужно еще две вещи: количество контр. точек (т.e. h +1) и степень (p), причем условие n > h >= p >= 1 должно выполняться. Таким образом, аппроксимация является более гибкой, чем интерполяция, потому что мы выбираем не только степень, но и количество контр. точек. Вот к чему, в итоге, сводится наша задача:

Глобальная Аппроксимация Кривой Дан набор из n +1 исходных точек, d₀, d₂,..., d _n, степень p, и число h, причем n > h >= p >= 1, нужно найти кривую B-spline степени p, определяемую h +1 конт. точками, которая бы удовлетворяла следующим условиям:

1. эта кривая содержит первую и последнюю исходные точки (т.e. d₀ и d _n) и
2. эта кривая аппроксимируется (т.е. приближается) к исходной ломаной по принципу наименьшей площади.

При наличии h и p, мы можем определить набор параметров и узловой вектор. Пусть параметры будут t ₀, t ₁,..., t_n. Заметьте, что количество параметров равно количеству исходных точек. Теперь, пусть аппроксимирующая кривая B-spline степени p будет

,

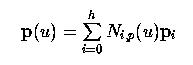где p ₀, p ₁,..., p _h - это h +1 неизвестных контр. точек. Так как нам нужно, чтобы кривая проходила через первую и последнюю исходные точки, то d ₀ = p (0) = p ₀, а d _n = p (1) = p _h. Таким образом, имеем всего h - 1 неизвестных контр. точек p ₁, p ₂,..., p _{h -1}. Принимая это во внимание, уравнение кривой становится следующим:

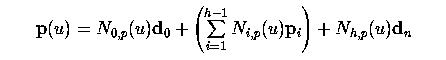
Дата добавления: 2015-10-29