Центростремительный Метод

E. T. Y. Lee предложил этот центростремительный метод. Допустим, мы ведем машину по извилистому спуску. Приходится быть очень аккуратными на крутых поворотах, чтобы ускорение по нормали (т.e. центробежная сила) не должно быть слишком большим. Иначе машина может потерять управление. Чтобы ехать безопасно, Lee предположил, что нормальная сила должна быть пропорциональна изменению угла. Центростремительный метод - это аппроксимация этой модели. Фактически, можно сказать, что центростремительный метод - это расширение метода длины хорды.

Пусть исходные точки равны d ₀, d ₁,..., d _n. Во-первых, нужно выбрать положительное значение "силы" a. Обычно a = 1/2 для извлечения квадратного корня. Затем, расстояние между двумя смежными точками вычисляется как | d _k - d _{k -1}| ^a, а не так, как обычно: | d _k - d _{k -1}|. Длина исходной ломаной по таким вычислениям равна

Отношение расстояний от d ₀ до d _k исходной ломаной по отношению к полной длине равно

Таким образом, L ₀ = 0, L ₁,..., L _n = 1 делят [0,1] в соответствии с длиной исходной ломаной по новым вычислениям. Отсюда, параметры равны

Если a = 1, то центростремительный метод становится методом длины хорды и, следовательно, первый является расширением последнего. Если a < 1, скажем, a = 1/2 (т.e. квадратный корень), | d _k - d _{k -1}| ^a меньше, чем | d _k - d _{k -1}|. Следовательно, влияние более длинной хорды (т.e. длина > 1) на длину исходной ломаной уменьшается, а влияние более короткой (т.e. длина < 1) - увеличивается. Из-за этой характеристики Lee решил, что центростремительный метод лучше подходит для прохождения крутых поворотов, чем метод длины хорды.

Давайте повторим пример, обсужденный в методе длины хорды. Имеем четыре исходные точки (n = 3): d ₀ = < 0,0 >, d ₁ = < 1,2 >, d ₂ = < 3,4 > и d ₃ = < 4,0 >. Возьмем a = 1/2 и длина каждой хорды по таким вычислениям будет

Полная длина равна

Таким образом, параметры равны

Далее идет распределения трех наборов параметров, вычисленных по методам равномерного распределения, длины хорды и центростремительному.

Взглянем на еще один пример. Далее показаны четыре исходных точки, интерполированные в три кривых B-spline по методу равномерного распределения (черный цвет), длины хорды (синий), и центростремительному (красный). Как видите, в методе равномерного распределения получается острый пик, а в методе длины хорды получается две больших выпуклости и две очень близких смежных точки хорошо интерполируются.

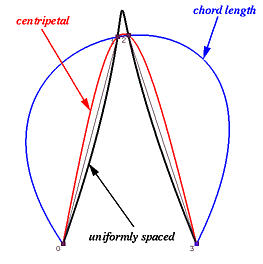
Можно ли сказать, что центростремительный метод лучше двух других? Следующий пример показывает, что не всегда. Имеем 7 исходных точек и черную, синюю и красную кривую, полученные соответственно по методам равномерного распределния, длины хорды и центростремительному методу. В данном случае метод равномерного распределения дает очень близкую интерполяцию. Центростремительный метод немного отстает от хорошего результата, который дает метод равномерного распределения. Ну а метод длины хорды вообще слишком выдается наружу.

Дата добавления: 2015-10-29