Получение Узлового Вектора

Когда получен набор параметров, можно найти узловой вектор. Пусть мы получили n +1 параметров t ₀, t ₁,..., t_n и степень p. Для кривой B-spline степени p, нам нужно m +1 узлов, где m = n + p +1. Если кривая фиксирована, то эти узлы равны u ₀ = u ₁ =.... = u_p = 0, u_{p +1},..., u_{m-p -1}, u_m-p = u_{m-p +1} =... = u_m = 1. Говоря точнее, первые p +1 и последние p +1 узлов равны 0 и 1, соответственно. Для оставшихся n-p узлов, их можно равномерно распределить или выбрать по каким-то другим соображениям.

Пусть оставшиеся n-p внутренних узлов равномерно будут распределены. Затем, u_p = 0, u_{p +1},..., u_{m-p -1}, u_m-p = 1 делят [0,1] на n-p +1 подинтервалов. Таким образом, узлы равны

Например, если есть 6 (n = 5) параметров, а степень равна p = 3, то нужно найти (n + p +1)+1 = (5+3+1)+1 = 10 узлов (т.e. m =9). Так как у нас фиксированная кривая, то первые и последние четыре (т.e. p +1) узлов должны быть равны 0 и 1, соответственно. Говоря точнее, имеем 0, 0, 0, 0, u ₄, u ₅, 1, 1, 1 и 1, а два внутренних узла делят [0,1] на три подинтервала, каждый из которых имеет длину, равную 1/3. Отсюда, узловой вектор равен { 0, 0, 0, 0, 1/3, 2/3, 1, 1, 1, 1}.

Равномерно распределенный узловой вектор не требует знания параметров и очень прост в нахождении. Тем не менее, этот метод не рекомендуется использовать, из-за того, что если он используется с методом длины хорды для глобальной интерполяции, то система линейных уравнений будет исключительной [?singular]

Другой известный метод получения узлового вектора, предложенный de Boor, состоит в "усреднении" параметров. Вот формула вычислений:

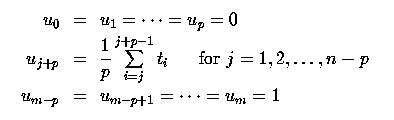
Таким образом, первый внутренний узел - это среднее из p параметров t ₁, t ₂,..., t_p; второй внутр. узел - среднее следующих p параметров, t ₂, t ₃,..., t_{p +1}. Пусть 6 (n = 5) параметров равны

t 0	t 1	t 2	t 3	t 4	t 5
	1/4	1/3	2/3	3/4

Нам нужно получить вектор для степени p = 3. Как упоминалось раньше, нужны 10 узлов (m = 9). Из этих десяти, первые четыре и последние четыре узла равны 0 и 1, соответственно. Таким образом, первый внутр. узел - это среднее из параметров 1/4, 1/3 и 2/3, а второй внутр. узел - это среднее следующих трех параметров 1/3, 2/3 и 3/4. Вычисленный узловой вектор равен

u 0 = u 1 = u 2 = u 3	u 4	u 5	u 6 = u 7 = u 8 = u 9
	(1/4+ 1/3 + 2/3)/3 = 5/12	(1/3 + 2/3 + 3/4)/3 = 7/12

Следующая схема показывает положения параметров и полученных узлов. Заметьте, что 0(4) и 1(4) значит, что 0 и 1 - это четверные узлы (т.e. множественности = 4). Как вы видите, первый ненулевой узловой интервал [0,5/12) содержит два параметра, второй ненулевой интервал [5/12,7/12) не содержит параметров, а третий интервал [7/12,1) - два параметра.

Дата добавления: 2015-10-29