
Читайте также:
|
б) Y2 =  ®
® 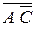 .
.
Решение. Используя закон Де Моргана и тождество (1.11), раскрываем скобки и избавляемся от инверсии:
 = (A
= (A  ) (
) (
 ) = A
) = A 
 .
.
 ®
® 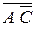 =
= 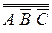 Ú
Ú 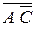 = A
= A 
 Ú (
Ú ( Ú C).
Ú C).
Ответ. Y2ДНФ = A 
 Ú
Ú  Ú C.
Ú C.
Пример 13.2. Пусть задана таблица булевой функции трех переменных. Записать для этой функции СДНФ и СКНФ.
Таблица 13.1.
| х 1 | х 2 | х 2 | Y |
Решение. Для записи совершенной дизъюнктивной нормальной формы (СДНФ) выбираем те наборы переменных x 1, x 2, x 3, при которых функция Y принимает значение равное 1:
YСДНФ = х 1 
 Ú
Ú  х 2
х 2  Ú х 1 х 2
Ú х 1 х 2  Ú
Ú  х 2 х 3.
х 2 х 3.
Соответственно для записи совершенной конъюнктивной нормальной формы (СКНФ) выбираются наборы переменных, при которых функция Y принимает значение равное 0:
СКНФ = (х 1 Ú x 2 Ú х 3) (х 1 Ú x 2 Ú  ) (
) ( Ú x 2 Ú
Ú x 2 Ú  ) (
) ( Ú
Ú  Ú
Ú  ).
).
Полученные выражения можно преобразовать к другому виду на основании свойств булевой алгебры.
Приведем функцию x  z Ú x
z Ú x  к СДНФ:
к СДНФ:
x  z Ú x
z Ú x  = x
= x  z Ú x
z Ú x  (y Ú
(y Ú  ) = x
) = x  z Ú x y
z Ú x y  Ú x
Ú x 
 .
.
Приведем к СКНФ:
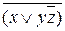 (x Ú z) =
(x Ú z) = 
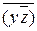 (x Ú z) =
(x Ú z) =  (
( Ú z) (x Ú z) = (
Ú z) (x Ú z) = ( Ú y
Ú y  ) (
) ( Ú z Ú x
Ú z Ú x  ) (x Ú z Ú y
) (x Ú z Ú y  ) = (
) = ( Ú y) (
Ú y) ( Ú
Ú  ) (
) ( Ú z Ú x) (
Ú z Ú x) ( Ú z Ú
Ú z Ú  ) (x Ú z Ú y) (x Ú z Ú
) (x Ú z Ú y) (x Ú z Ú  ) = (
) = ( Ú y Ú z
Ú y Ú z  ) (
) ( Ú
Ú  Ú z
Ú z  ) (x Ú
) (x Ú  Ú z) (
Ú z) ( Ú
Ú  Ú z) (x Ú y Ú z) (x Ú
Ú z) (x Ú y Ú z) (x Ú  Ú z) = (
Ú z) = ( Ú y Ú z) (
Ú y Ú z) ( Ú y Ú
Ú y Ú  ) (
) ( Ú
Ú  Ú z) (
Ú z) ( Ú
Ú  Ú
Ú  ) (x Ú
) (x Ú  Ú z) (
Ú z) ( Ú
Ú  Ú z) (x Ú y Ú z) (x Ú
Ú z) (x Ú y Ú z) (x Ú  Ú z) = (
Ú z) = ( Ú y Ú z) (
Ú y Ú z) ( Ú y Ú
Ú y Ú  ) (
) ( Ú
Ú  Ú
Ú  ) (
) ( Ú
Ú  Ú z) (x Ú
Ú z) (x Ú  Ú z) (x Ú y Ú z).
Ú z) (x Ú y Ú z).
13.2. Способы перехода от нормальных к совершенным нормальным формам
Существует два способа перехода от нормальных к совершенным нормальным формам булевых функций.
1. Аналитический способ.
Данный способ состоит в пошаговом дополнении каждой компоненты, составляющей нормальную форму до полной, т.е. содержащей все возможные переменные. Для СДНФ при этом производится операция последовательного умножения на логическое выражение вида (xi Ú 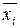 ), где xi - одна из переменных набора - x 1, x 2, x 3,..., xn, которые не входят в рассматриваемую компоненту.
), где xi - одна из переменных набора - x 1, x 2, x 3,..., xn, которые не входят в рассматриваемую компоненту.
В свою очередь, для СКНФ производится последовательное суммирование с логическим выражением вида xi 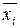 .
.
Причем количество проводимых операций умножения или суммирования зависит от разницы между числом переменных, входящих в рассматриваемую компоненту, и общим числом задействованных переменных.
Дата добавления: 2015-10-26; просмотров: 145 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Для выбора «лучшего» алгоритма необходимо получение оценок или границ для объема памяти и времени работы ЭВМ, которое потребуется алгоритму для обработки конкретных данных. 3 страница | | | Графический способ. |