Проверка условия i > 50. Если условие истинно, то перейти к пункту 8настоящего алгоритма, если условие ложно, то перейти к пункту 4.

8. Конец работы алгоритма.

Пример 10.5. Построить структурную схему алгоритма для подсчета среднего арифметического значения ряда целых четных чисел длины n, заданного в примере 10.2.

Решение: Подробное описание всех блоков структурной схемы алгоритма не приводится, поскольку блоки структурной схемы будут аналогичны операторам граф - схемы алгоритма из примера 10.2. Приведем содержание основных 1-го и 3 -го блоков.

Блок 1 - Ввод размера интервала n и начального значения шага i = 0;

Блок 3 - Выбор начального числа из интервала a;

Ответ. Структурная схема алгоритма показана на рис. 10.17.

Рис. 10.17. Пример структурной схемы алгоритма

10.5. “Жадные” алгоритмы

Для решения оптимизационных задач можно использовать класс алгоритмов, называемых “жадными”. В таком алгоритме на каждом шаге делается локально оптимальный выбор, в предположении, что итоговое решение окажется оптимальным. В общем виде, это не верно, но для многих оптимизационных задач такие алгоритмы позволяют получить локальный оптимум, а в частном случае - глобальный оптимум.

Рассмотрим стандартную задачу (Кормен, Лейзерсон, Ривест) о выборе заявок. Пусть даны n заявок на проведение занятий в одной и той же аудитории. Два разных занятия не могут проводиться в одно время. В каждой заявке указаны начало и конец занятия (s_i и f_i для i -той заявки). Разные заявки могут пересекаться, и тогда можно реализовать только одну из них. Каждая заявка отождествляется с промежутком [ s_i, f_i ], так что конец одного занятия может совпадать с началом другого, и это не считается пересечением. Целевая функция задачи заключается в наборе максимального количества совместных друг с другом заявок при временных ограничениях и граничных условиях. Жадный алгоритм работает следующим образом. Предполагаем, что заявки упорядочены в порядке возрастания времени окончания, т.е., f₁ ≤ f₂ ≤ … £ f_n. Заявки с одинаковым временем конца располагаем в произвольном порядке. Тогда запишем псевдокод алгоритма, приведенный в учебнике (Кормен, Лейзерсон, Ривест):

ВЫБОР ЗАЯВОК (s, f - массивы)

1 n ← length [ s ]

2 А ← {1}

3 j ← 1

4 for i ← 2 to n

5 do if s_i ≥ f_j

6 then A ← A È { i }

7 j ← i

8 return A

Множество А состоит из номеров выбранных заявок, j – номер последней из них; при этом f_j = mах{f_k: kÎA}, поскольку заявки отсортированы по возрастанию времени окончания. Вначале А содержит заявку номер 1, и j = 1 (строки 2 - 3). Далее (цикл в строках 4 - 7) ищется заявка, начинающаяся не раньше окончания заявки номер j. Если таковая найдена, она включается в множество А и переменной j присваивается ее номер (строки 6 - 7). Описанный алгоритм выбора заявок требует всего лишь O (n) шагов (не считая предварительной сортировки). Как и подобает жадному алгоритму, на каждом шаге он делает выбор так, чтобы остающееся свободным время было максимально.

Говорят, что к оптимизационной задаче применим принцип жадного выбора, если последовательность локально оптимальных (жадных) выборов дает глобально оптимальное решение.

Отметим, что задачи, решаемые с помощью жадных алгоритмов, должны обладать свойством оптимальности для подзадач. А именно, оптимальное решение всей задачи содержит в себе оптимальные решения подзадач.

10.6. Нечеткие (расплывчатые) алгоритмы

Нечеткий (расплывчатый) алгоритм — это упорядоченное множество расплывчатых инструкций, которые при их реализации позволяют получать приближенное решение задач.

Инструкции в расплывчатых алгоритмах делят на три группы.

1-я группа — назначающие инструкции. Например, х = “большой” или х = “вкусный”.

2-я группа — расплывчатые высказывания. Например, если х — “очень дорогой”, то перейти к y, или если х “не помещается в комнате”, то “увеличить размер комнаты”.

3-я группа — безусловные активные предложения. Например, “немного увеличить” х, или “сильно увеличить” х, или перейти к другому значению параметра x.

Отметим, что все инструкции могут быть нечеткими или четкими.

Нечеткие алгоритмы определения — это конечное множество инструкций, определяющих расплывчатое множество в терминах других расплывчатых множеств или дающих метод для определения степени принадлежности каждого элемента для определяемого множества. Алгоритмы идентификации устанавливают степень принадлежности элементов множеству. Алгоритмы порождения используются для порождения новых, а не для определения данных расплывчатых множеств. Примерами таких алгоритмов могут служить алгоритмы сочинения стихов, конструирования ЭВА, разработки технических заданий на изделие. Нечеткиеалгоритмы, используемые для описания поведения произвольной системы, называются бихевиористическими.

Расплывчатой переменной считают кортеж П = < a, X, >, где a — наименование расплывчатой переменной; X = {x₁, х ₂,..., х_n } — область ее определения; A = { 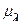(x_i) | x_i } x_i Î X — расплывчатое множество в X, определяющее ограничения на возможные значения П. Лингвистической переменной называют кортеж Л = < b, Т, X >, где b — наименование Л; Т — множество ее значений, представляющих наименования П, областью определения которых является X.

Например, пусть оценивается качество технологического процесса выхода годных с помощью понятий “плохой”, “средний”, “хороший”. Максимальный выход годных 80%. Тогда Л = <качество, Т, [0; 80]>, где Т = {“плохой”, “средний”, “хороший”}. Значения Л описываются расплывчатыми переменными. Например, значение “плохой” описывается расплывчатой переменной < плохой, [0; 80], >, где может иметь вид = {< 1 / 0 >,
< 0,8 / 5 >,< 0,6 / 7 >,< 0,2 / 20 >}. Значение “хороший” можно, например, описать так: < хороший, [0; 80], >, где = {< 1 / 80 >, < 0,8 / 75 >, <0,6 / 70 >,< 0,2 / 40 >}.

Функцию принадлежности при наличии k экспертов упрощенно определяют так. Пусть k ₁ экспертов на вопрос о принадлежности х Î Х к отвечают положительно, а k ₂ = k — k ₁ экспертов на этот же вопрос отвечают отрицательно. Тогда устанавливают следующее значение функции принадлежности: 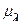(x_i) = k ₁ / { k ₁ + k ₂). Для точных оценок приводят парные сравнения функций принадлежности и др. Лингвистические переменные используют для построения расплывчатых моделей и алгоритмов.

Например, приведем нечеткий алгоритм. Пусть у — быстродействие системы, состоящей из двух ЭВМ, а х — быстродействие одной ЭВМ в системе.

Тогда запишем следующий нечеткий алгоритм построения системы с заданным быстродействием:

1°. Если х “мало” и х “незначительно увеличить”, то у “незначительно увеличится”.

2°. Если х “мало” и х “значительно увеличить”, то у “увеличится значительно”.

3°. Если х “велико” и х “увеличить значительно”, то у “увеличится очень значительно”.

Заметим, что значения расплывчатых условных предложений в этом алгоритме можно определить, если даны значения первичных терминов «большой», «маленький» и расплывчатых терминов «незначительно», «значительно», «очень значительно». Значения указанных терминов субъективны и зависят от носителя нечеткого множества. Например, если четкое множество X = {1, 2, 3, …, 10}, то при x = 9 мы имеем, скорее всего, термин «большой». Если четкое множество X = {1, 2, 3, …, 1000}, то при x = 9 мы имеем, скорее всего, термин «маленький».

Нечеткий алгоритм, который служит для получения приближенного описания стратегии и решающего правила, называется нечетким алгоритмом принятия решений. К такому классу можно отнести алгоритмы принятия решений при пересечении перекрестка, компоновке кристаллов интегральной микросхемы, определении жизненного цикл изделий и др. На рис. 10.18 приведена структурная схема нечеткого алгоритма трассировки (определения путей между частями интегральной схемы).

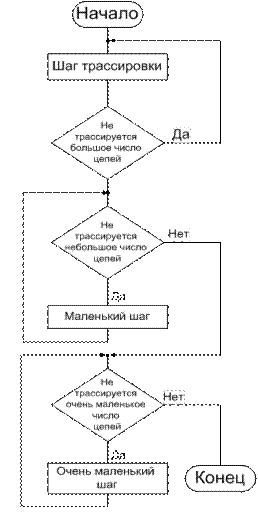
Рис. 10.18. Структурная схема нечеткого алгоритма «Трассировка»

Эту структурную схему (рис. 10.18) можно представить в виде следующих нечетких инструкций:

1°. Сделать шаг трассировки. Если не трассируется “большое” число связей, то перейти к 1°.

2°. Если не трассируется “небольшое” число связей, то сделать “малый” шаг и перейти к 2°.

3°. Если не трассируется “очень маленькое” число связей, то сделать “очень маленький шаг” и перейти к 3°.

4°. Конец работы алгоритма.

Рассмотрим пример размещения БИС на подложке. Структурная схема одного из возможных алгоритмов такого типа показана на рис. 10.19. В терминах нечетких высказываний структурная схема алгоритма может быть переведена в расплывчатые инструкции.

Рис. 10.19. Структурная схема расплывчатого алгоритма размещения

Следует отметить, что конструктор хорошо оперирует расплывчатыми понятиями «большое», «маленькое», «очень маленькое» и эффективно реализует данный алгоритм в интерактивном режиме связи с ЭВМ. При определении степени принадлежности можно формализовать алгоритм и реализовать его на ЭВМ. Отметим, что операция «сделать шаг» в алгоритме (рис. 10.18) может быть сложным алгоритмом перетрассировки всего кристалла или небольшой его области, или простого удаления нескольких трасс и т.п. Реальные варианты нечетких алгоритмов представляют сложную структуру и необходимо разбиение его на части меньшей размерности. Важным в разработке и применении таких алгоритмов является то, что они могут служить эффективным средством распространения и изучения опыта пользователя.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Назовите основные виды универсальных алгоритмических моделей.

2. Что представляет собой первая алгоритмическая модель?

3. В чем заключается преобразование слов в произвольных абстрактных алфавитах?

4. Что такое алфавитный оператор?

5. Дайте различные определения алгоритма на основе первой алгоритмической модели.

6. Какие алгоритмы являются равными, а какие – эквивалентными?

7. Определите вторую алгоритмическую модель.

8. Каким образом строятся рекурсивные алгоритмы?

9. Что такое алгоритмы, сопутствующие рекурсивным функциям?

10. Что такое рекурсивные и частично рекурсивные функции?

11. Определите операторы суперпозиции, подстановки и рекурсии.

12. Сформулируйте тезис Черча.

13. В чем заключается метод «разделяй и властвуй»?

14. Постройте третью алгоритмическую модель

15. Опишите принцип работы машины Тьюринга.

16. Приведите правила построения алгоритмов Ван-Хао.

17. Приведите основные правила построения логических схем алгоритмов (ЛСА).

18. В чем заключаются правила построения алгоритмов Маркова?

19. Определите основную идею графических схем алгоритмов (ГСА).

20. Приведите основные правила построения структурных схем алгоритмов.

21. В чем основная идея словесного описания алгоритма?

22. Что представляют собой «жадные» алгоритмы?

23. Для каких задач целесообразно применять «жадные» алгоритмы?

24. Дайте определение нечеткого (расплывчатого) алгоритма.

25. Что такое расплывчатая и лингвистическая переменные?

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

1. Постройте пример первой алгоритмической модели.

2. Постройте пример второй алгоритмической модели.

3. Постройте пример третьей алгоритмической модели.

4. Запишите словесный алгоритм упорядочивания массива из n чисел в порядке возрастания.

5. Запишите словесный алгоритм для вычисления среднего арифметического и наибольшего значений элементов массива целых чисел размерностью до 70.

6. Запишите алгоритм Ван-Хао для вычисления среднего арифметического значения элементов массива чисел размерностью до 20.

7. Составить словесный алгоритм определения элементов множества Z, если Z = X \ Y, где X, Y - множества (| X | = N, | Y | = M).

8. Составить ЛСА поисканаибольшегоэлемента массива A_ij, где i = 1, 2,...,10; j = 1, 2,..., 20.

---

Дата добавления: 2015-10-26