Если область прибытия соответствия совпадает с его областью отправления, то соотвествие преобразуется в отношение.

Совершенство только тогда совершенство, когда оно представляется достижимым только в бесконечности и когда поэтому возможность приближения к нему бесконечна.

Л. Толстой

Глава 6. Упорядоченные бесконечные множества

Понятие упорядоченного бесконечного множества, определение и способы их задания, интервал, сегмент, соответствие подобия, сечение, скачок, щель, дедекиндово сечение, принцип трансфинитной индукции, проблема континуума, счетные и несчетные множества, мощность континуума, алгебраические и трансцендентные числа.

ЦЕЛИ

Освоив эту главу, студенты должны:

· знать основные сведения об упорядоченных бесконечных множествах;

· иметь понятия об интервале и сегменте;

· уметь определять 4 типа сечений;

· уметь строить счетные и несчетные множества;

· знать, что представляет собой проблема континуума;

· иметь понятие о парадоксах в теории множеств;

· иметь понятие о принципе трансфинитной индукции и уметь применять его на практике.

6.1. Основные сведения об упорядоченных бесконечных множествах

Простейшим примером упорядоченных бесконечных множеств (УБМ) является множество всех целых чисел, натуральных, рациональных, неотрицательных и так далее чисел. Одно и то же бесконечное множество можно упорядочить различными способами.

Пусть множество Х является УБМ, причем элементы a, b, x Î X. Если справедлива запись а ® х и х ® b (a ® x ® b), то говорят, что элемент х лежит между элементами a и b. Множество всех элементов, лежащих между a и b, называется интервалом (a, b) упорядоченного бесконечного множества Х.

Если к интервалу (а, b) добавить два его конца, т.е. элементы a и b, то получим сегмент [a, b]. Два элемента a и b множества Х называются соседними, если интервал (a, b) — пустой. Если элемент из упорядоченного бесконечного множества Х таков, что ("xÎX)(x¹a Ù aÞx),то а является первым или наименьшим элементом Х.

В противоположном случае, если ("xÎX)(x¹a Ù хÞа), то тогда а является наибольшим элементом.

Очевидно, что в каждом УБМ может быть не больше одного наименьшего и одного наибольшего элемента. Например, в множестве положительных чисел наименьшим элементом будет ноль. Соответственно в множестве неположительных чисел ноль — наибольший элемент.

Для отношения порядка в УБМ справедливо следующее выражение:

x Þ y ® f(x) Þ f(y).

Другими словами, взаимно-однозначное отображение УБМ Х на УБМ Y сохраняет порядок, т.е. х ® y влечет, что f(x) ® f(y), где xÎX, yÎY. Такое отображение часто называют соответствием подобия. Очевидно, что два подобных упорядоченных бесконечных множества эквивалентны между собой.

Введем понятие сечения. Сечением упорядоченного бесконечного множества Х называется разбиение этого множества на два непустых подмножества А и В таких, что каждый элемент одного множества низшего класса всегда предшествует каждому элементу второго множества верхнего класса.

Существует 4 типа сечений.

1. В нижнем классе А есть наибольший элемент (а), а в верхнем классе В есть наименьший элемент (b). Такое сечение называется скачком. В этом случае интервал (а, b) является пустым.

2. В нижнем классе А есть а, а в верхнем классе В нет b.

3. В нижнем классе А нет а, а в верхнем классе В есть b. Второй и третий классы называются дедекиндовыми сечениями.

4. В нижнем классе А нет а, а в верхнем классе В нет b. Такое сечение называется щелью.

Рассмотрим принцип трансфинитной индукции.

Пусть дано упорядоченное бесконечное множество Х и имеется высказывание Р = Р(х), которое зависит от этого множества. Если высказывание Р верно для первого элемента х₀ÎХ и если из того, что оно верно для всех элементов хÎХ, предшествующих данному, следует, что предположение Р верно и для элемента х’, то высказывание Р верно для любого элемента, принадлежащего множеству Х.

Когда множество Х является множеством натуральных чисел, принцип трансфинитной индукции превращается в обычный принцип полной индукции.

Приведем пример. Докажем по индукции, что равенство

выполняется при всех натуральных n.

Пусть P (n) – предикат . При n = 1 левая часть равна ½, а правая часть (1(1 + 1) / 4 также равна ½. Следовательно, выражение при P (1) – истинно.

Предположим, что равенство 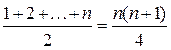справедливо для произвольного числа m. Тогда

Тогда при любом натуральном m импликация P (m) ® P (m +1) истинна. Следовательно, на основании принципа математичыеской индукции мы показали, что предикат P (n) – истина для любых натуральных n.

Приведем ряд известных положений об УБМ.

Каждое множество, содержащее бесконечное подмножество, бесконечно. Тогда очевидно, что множество всех подмножеств бесконечного множества также бесконечно.

Каждое УБМ имеет собственное подмножество, которому оно равномощно и наоборот, если множество равномощно своему подмножеству, то оно является бесконечным.

Никакое множество не является равномощным множеству всех своих подмножеств.

Произвольное множество называется не более, чем счетным, если оно конечно или равномощно множеству натуральных чисел.

Георг Кантор предположил способ сравнения двух упорядоченных бесконечных множеств, основанный на установлении взаимно-однозначного соответствия между элементами этих множеств. Это выполняется объединением элементов одного множества в пары с элементами другого множества так, что каждый элемент входит в одну единственную пару.

Если для двух УБМ установлено взаимно-однозначное соответствие, то эти множества равнозначны, т.е. имеют одинаковое количество элементов или |A| = |B|.

В УБМ встречаются парадоксы.

Например, некоторые множества могут быть равномощными своей части. Например, можно установить взаимно-однозначное соответствие между множеством натуральных чисел N и множеством их квадратов.

N 0, 1, 2, 3, 4, 5,...

N² 0, 1, 4, 9, 16, 25,...

В теории множеств натуральный ряд чисел принят за эталон класса бесконечных множеств.

6.2. Проблема континуума

Любое множество, равномощное натуральному ряду, называется счетным. Считают, что множество действительных чисел является несчетным множеством.

Множество, равномощное множеству действительных положительных чисел, не превосходящих единицы, называется множеством мощности континуума или континуальным.

Пусть имеем множество натуральных чисел. Тогда обозначим через N его мощность. Обозначим через К мощность множества действительных положительных чисел не превосходящих единицы.

Пусть имеется произвольное бесконечное множество М. Тогда мощность |M| равна произвольному числу m. В этом случае число всех подмножеств множества М будет равно 2^m.

Покажем теперь, что несчетные множества существуют и причем с различными мощностями. Эталоном несчетного множества является множество точек на прямой линии. Покажем, что множество всех точек на прямой линии несчетно.

Рассмотрим множество всех действительных чисел, т.к. каждой точке прямой можно поставить в соответствие одно действительное число и наоборот. Каждое действительное число запишем в виде бесконечной дроби вида 0, a₁ a₂ a₃.... Предположим, что удалось пронумеровать все действительные числа. Для опровержения этого предположения надо найти хотя бы одно не пронумерованное действительное число.

Согласно известной эвристике способ построения заключается в использовании двух правил:

Если a=1, то ставят 2.

Если a¹1, то ставят 1.

Возьмем ноль и поставим после него запятую. Рассмотрим первую цифру, если эта цифра отлична от 1, то в соответствующий ей разряд ставим 1, иначе 2. И далее процесс продолжается аналогично до просмотра всего действительного числа. Очевидно, что построенное число не получило никакого номера, т.к. в первом десятичном знаке оно отличается от числа с номером 1, во втором — от числа с номером 2, в n-знаке — от числа с номером n и т.д.

Например, имеем несколько действительных чисел:

1) 0, 2 7 3 6 1...

2) 0, 4 1 1 2 2...

3) 0, 6 7 3 1 1...

4) 0, 7 1 1 4 4...

5) 0, 9 1 8 1 9...

Тогда число, не получившее никакого номера, может иметь такой вид 0,12111...

В упорядоченных бесконечных множествах выделяют понятия алгебраического и трансцендентного числа. А лгебраическими называются числа, которые являются корнями уравнения вида a₀xⁿ + a₁x^n-1 +... + a_kx + a_k+1 = 0, т.е. корнями уравнений с целыми коэффициентами. Числа, которые не являются корнями таких уравнений, называются трансцендентными числами. Известным трансцендентным числом является число p» 3,14159...

Оказалось, что алгебраических чисел относительно мало (т.к. это счетные множества), а трансцендентных относительно много (это несчетные множества). Луи Виль привел алгоритм построения трансцендентных чисел. Он заключается в том, что в заданном действительном числе после первой единицы ставят ноль, после второй – два нуля, после третьей шесть, после n-ой – n! нулей. Примером трансцидентного числа является число 0,101000100000001...

Существует утверждение, что на коротком и длинном отрезке точек поровну. Это следует из того, что всегда можно установить взаимно-однозначное соответствие между точками любых отрезков. Следовательно, любая геометрическая фигура, содержащая хоть одну линию, имеет столько же точек, сколько и отрезок!

Множества точек, расположенных на отрезках, получили название множество мощности континуума (Континуум — от лат. непрерывный). Множество мощности континуума самое большое несчетное множество.

Проблема континуума заключается в попытке ответить на вопрос: существует ли промежуточное множество, у которого больше элементов, чем множество натуральных чисел, и меньше элементов, чем множество точек на прямой.

Рассмотрим некоторые операции над мощностями конечных и бесконечных множеств. Часто мощность множества |M| = m называют кардинальным числом и обозначают card M = m.

Пусть заданы конечные множества А и В, |A| = m, |B| = n, N — мощность множества натуральных чисел (счетного множества), К — мощность несчетного множества (континуума).

Отметим, что мощности можно складывать так же, как складывают натуральные числа.

Тогда имеем

1. m + n = n + m,

2. m + N = N,

3. N + N = N,

4. N + K = K,

5. K + K = K.

Второе выражение означает, что сумма конечного и счетного множеств является счетным множеством. Третье выражение означает, что сумма мощностей счетных множеств равна мощности счетного множества. Четвертое выражение означает, что сумма мощности счетного множества и множества мощности континуума дает множество мощности континуума. Пятое выражение означает, что сумма множеств мощности континуума дает множество мощности континуума.

Аналогичные выражения существуют при декартовом произведении мощностей

6. m x n = n x m,

7. N x N = N,

8. N x K = K,

9. K x K = K.

Седьмое выражение означает, что если множества счетные, то и множества всех пар из этих множеств счетно. Это другая формулировка утверждения, что сумма счетных множеств является счетным множеством. Равенство (9) означает, что число точек на отрезке и в квадрате одно и то же (например, пусть к – это число точек на отрезке, тогда к х к – число точек в декартовом произведении отрезка на себя, т.е. число точек в квадрате).

Очевидно, что все натуральные числа содержатся среди кардинальных чисел, но существуют кардинальные числа, не являющиеся натуральными. Приведем ряд известных теорем Кантора, доказательство которых приведено в специальной литературе, указанной в конце данной части.

Теорема 1. Для любого кардинального числа m справедливо неравенство m < 2^m.

Теорема 2. Мощность m’ подмножества множества, имеющего мощность m, удовлетворяет неравенству m’ £ m.

В теории множеств обнаружены противоречия (парадоксы), называемые антиномией. Приведем наиболее популярные из них.

Дата добавления: 2015-10-26