Ответ: Мы доказали, что A Í B влечет, что Í .

Пример 2.5. Доказать, используя метод взаимного включения, закон дистрибутивности пересечения относительно объединения:

A Ç (B È C) = (A Ç B) È (A Ç C).

Для доказательства этого тождества необходимо доказать, чтоA Ç (B È C) Í (A Ç B) È (A Ç C), a затем что(A Ç B) È (A Ç C) Í A Ç (B È C).Докажем первое включение, показывая истинность последовательности импликаций.

1. Необходимость.

(" x Î Е)(x Î (A Ç (B È C)) ® x Î A & (x Î B Ú x Î C) ®

(импликация истинна на основе определения операций объединения и пересечения)

x Î A & x Î B Ú x Î A & x Î C ® x Î (A Ç B) Ú x Î (A Ç C) ®

(использован дистрибутивный закон)

x Î ((A Ç B) È (A Ç C)) ® A Ç (B È C) Í (A Ç B) È (A Ç C).

(использовано определение включения в высказывательной форме)

Таким образом, доказано прямое включение множеств (необходимость).

2. Достаточность. Теперь докажем обратное включение:

(" x Î Е)(x Î ((A Ç B) È (A Ç C))) ® x Î (A È B) Ú x Î (A È C) ®

x Î A & x Î B Ú x Î A & x Î C ®

x Î A & (x Î B Ú x Î C) ®

x Î A & x Î B È C ® x Î (A Ç (B È C)) ®

(A Ç B) È (A Ç C) Í A Ç (B È C).

Обратное включение также доказано.

Ответ: Таким образом, дистрибутивность пересечения относительно объединения доказана.

Пример 2.6. Доказать, используя геометрический метод, закон дистрибутивности объединения относительно пересечения:

A È (B Ç C) = (A È B) Ç (A È C).

Для доказательства заданного тождества отметим на диаграмме рис. 2.8,а множество точек, соответствующих множеству A È (B Ç C),а на диаграмме рис. 2.8,б - множество точек, соответствующих множеству (A È B) Ç (A È C).

На рис. 2.8,а светлой штриховкой отмечено множество В Ç С, а серой штриховкой - множество А, множество A È (B Ç C) на диаграмме представлено фигурой, представляющей собой объединение фигур, заштрихованных вышеуказанным образом.

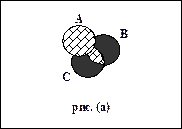
Рис. 2.8. Пример диаграммы Эйлера-Венна

На рис. 2.8,б множество A заштриховано серым, множество B - черным, а множествоC - белым цветом, тогда объединение множеств A È Bпредставляет собой фигуру, объединяющую серый и черный круги, объединение множеств A È C – фигуру, объединяющую серый и белый круги, а пересечение множеств A È Bи A È C представлено множеством A и множеством точек внутри фигуры, имеющей одинаковую с множеством A штриховку.

Ответ: Сравнивая эти два рисунка, можно сделать вывод, что эти множества равны, следовательно, тождество доказано.

Пример 2.7. Доказать, используя метод от противного, истинность тождества:

A Ç (B \ A) = Æ.

Решение: Предположим, что A Ç (B \ A) ¹ Æ, т.е. существует элемент х, принадлежащий множеству, стоящему в левой части тождества. Покажем с помощью последовательных импликаций, что наше предположение ложно:

($ x)(x Î (A Ç (B \ A)) ® x Î A & x Î (B \ A) ®

x Î A & (x Î B & x Ï A) ® x Î A & x Î B & x Ï A ®Æ & x Î B ® Æ

(использовано свойство коммутативности)

Ответ: Таким образом, исходное тождество доказано.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1. Что такое взаимное включение множеств и в каком случае существует взаимное включение?

2. Что называется объединением, пересечением, разностью и дополнением множеств?

3. В каком случае объединение, пересечение и разность двух множеств равны пустому множеству?

4. Как определяется симметрическая разность множеств?

5. Привести примеры множеств:

а) объединение которых равно их пересечению;

б) пересечение множеств равно Æ, а их разность не является пустым множеством.

6. Приведите основные тождества алгебры множеств.

7. Поясните операцию дополнения множеств.

8. Какие методы доказательства тождеств с множествами вам известны?

9. Что представляет из себя метод доказательства тождеств с множествами от противного?

10. На чем основан метод взаимного включения?

11. На чем основан геометрический метод доказательства тождеств с множествами?

ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ

1. Пусть множества А, В и С являются подмножествами множества S = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}, A = {1, 2, 3, 4, 5, 10}, B = {2, 4, 7, 8, 9}, C = {5, 8, 10}.

Найти: A È B, A \ C, 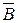Ç (A È C).

2. Пусть A = { x | x - женское имя}; B = {Мария, Иван, Петр, Иванов}; C = { x | x - фамилия}.

Найти: A Ç B, A Ç C, B Ç C.

3. Показать, что для записи последовательности операций объединения и разности необходимы круглые скобки.

4. Показать на диаграммах Эйлера-Венна справедливость утверждения задания 3.

5. Доказать, что B Í A & C Í A Þ B È C Í A.

6. Выполнить разбиения множества В на 5 классов: B = { a, b, c, 1, 2, 3}.

7. Для произвольных множеств А, В, С Î Â(E) доказать или опровергнуть следующие тождества методом включения множеств.

а) A È (B Ç C) = (A È B) Ç (A È C);

б) ;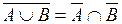

в) ;

г) A \ B = A \ (A Ç B);

д) A \ B = A Ç ;

е) A \ (A \ B) = A Ç B;

ж) A Ç (B \ C) = (A Ç B) \ (A Ç C);

з) (A È B) Ç (B È C) Ç (A È C) = (A Ç B) È (B Ç C) È (A Ç C);

и) А \ (В È С) = (А \ В) Ç (А \ С);

к) А \ (В Ç С) = (А \ В) È (А \ С);

л) A \ (B \ C) = (A \ B) È (AÇBÇC);

м) A Ç (B \ C) = (A Ç B) \ (A Ç C);

н) A È (B \ C) = (A È B) \ (A È C).

8. Для произвольных А, В, С Î Â(E) доказать или опровергнуть следующие тождества методом от противного.

а) (A \ (A \ B)) \ (A Ç B) = Æ;

б) А Ç (В \ А) = Æ;

в) (A Ç C) \ (С \ (С \ A) = Æ;

г) (A \ С) \ (A Ç 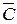) = Æ;

д) ;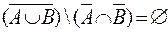

е) ;

ж) ((А Ç В) È (А Ç 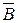)) \ А = Æ.

9. Докажите, что B È C = Æ, еслиB = Æ и C = Æ.

10. Покажите на примере, что выражение A È B Ç C требует использования круглых скобок.

11. Докажите что если B Í A & C Í A, то B È C Í A;и еслиAÍ B & A Í C, тоA Í B Ç C.

12. Докажите, что если C Í A, тоB Ç C Í A и C Í A È B.

13. Докажите, Â(A) Ç Â(B) = Â(A Ç B).

14. Справедливо ли тождество Â(A) È Â(B) = Â(A È B).Если нет приведите пример.

15. Справедливо ли тождество: { x | x Î Z & x = 2 m } Ç { x | x Î Z & x = 3 m } = { x | x Î Z & x = 6 m }, где m Î N.

16. Опровергните следующее утверждение: если А Ç В = А Ç С, то В = С.

17. Пусть

I - множество целых чисел, I = {...-1, 0, 1,...};

N - множество положительных целых чисел N = {0, 1, 2,...};

Np- множество отрицательных целых чисел Np= {..., -2, -1, 0};

E - множество четных чисел;

P - множество простых чисел.

Найдите: N Ç Np, I \ N, I \ Np, N È Np, I \ E, E Ç P.

18. Доказать, что А = В, следуя каждому из следующих условий:

а) A \ B = B \ A;

б) A È B = B Ç A;

в) A È C = B È C & A Ç C = B Ç C.

19. Доказать, что , если только A = Æи .

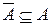20. Используя диаграммы Венна, рассмотрите совместимость следующих утверждений.

а) (A Ç B) È C = A \ B и C Ç A = B Ç A;

б) (A \ (B \ C)) Í C È B и A Ç B Ç C = Æ и C \ B Í A;

с) (B \ A) Ç C ¹ Æ и C \ A Í C \ B.

21. Докажите следующие тождества:

а) (A È B) Ç (C È D) = (A Ç C) È (A Ç D) È (B Ç C) È (B Ç D);

б) А \ В = È (А Ç В);

в) А \ (А \ (А \ В)) = А \ В;

г) А \ (А \ (А \ (А \ В))) = А Ç В;

д) A₁ È A₂ È... È A_n = (A₁ \ A₂) È (A₂ \ A₃) È... È (A_n-1 \ A_n) È (A_n \ A₁) È (A₁ Ç A₂ Ç... Ç A_n) = A₁ È (A₂ \ A₁) È (A₃ \ (A₁ È A₂)) È (A₄ \ (A₁ È A₂ È A₃)) È... È (A_n \ (A₁ È A₂ È... È A_n-1)).

е) A₁ Ç A₂ Ç... Ç A_n = A₁ \ [(A₁ \ A₂) È (A₁ \ A₃) È... È (A₁ \ A_n)]

22. Упростите следующие выражения:

а) ;

б) .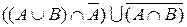

Дата добавления: 2015-10-26