
Читайте также:
|
Пример 8.3. Заданы нечеткие множества  = {<0.6; x1>; <0.3; x2>; <0.8; x4>; <0.4; x5>} и
= {<0.6; x1>; <0.3; x2>; <0.8; x4>; <0.4; x5>} и  = {<0.2; x2>; <0.5; x3>; <0.7; x4>; <0.9; x5>} на множестве X = {x1, x2, x3, x4, x5}.
= {<0.2; x2>; <0.5; x3>; <0.7; x4>; <0.9; x5>} на множестве X = {x1, x2, x3, x4, x5}.
Найти степень включения нечеткого множества  в
в  .
.
Решение. n(  ,
,  ) = (0.6 ® 0) & (0.3 ® 0.2) & (0 ® 0.5) & (0.8 ® 0.7) & (0.4 ® 0.9) = 0.4 & 0.7 & 1 & 0.7 & 0.9
) = (0.6 ® 0) & (0.3 ® 0.2) & (0 ® 0.5) & (0.8 ® 0.7) & (0.4 ® 0.9) = 0.4 & 0.7 & 1 & 0.7 & 0.9
Ответ: Степень включения нечеткого множества  в
в  равна n(
равна n(  ,
,  ) = 0.4.
) = 0.4.
Пример 8.4. Заданы нечеткие множества  = {<0.4; x1>; <0.7; x2>; <0.2; x4>; <0.9; x5>} и
= {<0.4; x1>; <0.7; x2>; <0.2; x4>; <0.9; x5>} и  = {<0.6; x3>; <0.3; x4>; <0.8; x5>} на множестве X = {x1, x2, x3, x4, x5}.
= {<0.6; x3>; <0.3; x4>; <0.8; x5>} на множестве X = {x1, x2, x3, x4, x5}.
Найти пересечение, объединение и разность этих множеств, а также дополнение множества  .
.
Ответ:  Ç
Ç  = {<0.2; x4>; <0.8; x5>};
= {<0.2; x4>; <0.8; x5>};
 È
È  = {<0.4; x1>; <0.7; x2>; <0.6; x3>; <0.3; x4>; <0.9; x5>};
= {<0.4; x1>; <0.7; x2>; <0.6; x3>; <0.3; x4>; <0.9; x5>};
 \
\  = {<0.4; x1>; <0.7; x2>; <0.2; x4>; <0.2; x5>};
= {<0.4; x1>; <0.7; x2>; <0.2; x4>; <0.2; x5>};
ù  = {<1; x1>; <1; x2>; <0.4; x3>; <0.7; x4>; <0.2; x5>}.
= {<1; x1>; <1; x2>; <0.4; x3>; <0.7; x4>; <0.2; x5>}.
Пример 8.5. Задать различными способами произвольное соответствие  = (X, Y,
= (X, Y, 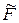 ).
).
Решение:
а) Пусть заданы конечные множества X = {x1, x2, x3, x4}; Y = {y1, y2, y3, y4}; 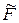 = {<0.3; <x1; y1>>; <0.2; <x1; y3>>; <0.4; <x2; y2>>; <0.6; <x3; y2>>; <0.1; <x4; y1>>; <0.8; <x4; y4>>}. Тогда можно сказать, что задано нечеткое соответствие
= {<0.3; <x1; y1>>; <0.2; <x1; y3>>; <0.4; <x2; y2>>; <0.6; <x3; y2>>; <0.1; <x4; y1>>; <0.8; <x4; y4>>}. Тогда можно сказать, что задано нечеткое соответствие  = (X, Y,
= (X, Y, 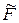 ) теоретическим способом.
) теоретическим способом.
б) То же соответствие, заданное матричным способом, будет иметь следующий вид:

 ,
,
где строки матрицы соответствуют элементам множества X, а столбцы – элементам множества Y. Элементы матрицы принимают значения, равные степени принадлежности элементов множества X ´ Y множеству 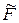 .
.
в) Графический способ (рис. 8.7). Графически нечеткое соответствие может быть задано в виде ориентированного двудольного взвешенного графа, где вес ребра соответствует значению степени принадлежности элемента множеству 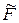 .
.

Рис. 8.7. График соответствия 
Пример 8.6. Заданы нечеткие соответствия  = (X, Y,
= (X, Y, 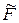 ) и
) и  = (Y, Z,
= (Y, Z,  ). График соответствия
). График соответствия  изображен на рис. 8.7, а график соответствия
изображен на рис. 8.7, а график соответствия  - на рис. 8.8. Найти композицию этих соответствий.
- на рис. 8.8. Найти композицию этих соответствий.

Рис. 8.8. График соответствия 
Ответ: Композиция соответствий  и
и  показана на рис. 8.9.
показана на рис. 8.9.

Рис. 8.9. Результат композиции соответствий  и
и 
Пример 8.7. Задать произвольное нечеткое отношение 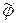 .
.
Ответ: а) Теоретический способ. 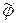 = (X,
= (X, 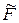 ); X = {x1, x2, x3, x4};
); X = {x1, x2, x3, x4}; 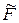 = {<0.4; < x1, x2>>; <0.7; < x1, x3>>; <0.2; < x2, x1>>; <0.5; < x2, x4>>; <0.7; < x3, x2>>; <0.3; < x3, x4>>; <0.8; < x4, x2>>; <0.1; < x4, x3>>}.
= {<0.4; < x1, x2>>; <0.7; < x1, x3>>; <0.2; < x2, x1>>; <0.5; < x2, x4>>; <0.7; < x3, x2>>; <0.3; < x3, x4>>; <0.8; < x4, x2>>; <0.1; < x4, x3>>}.
б) Матричный способ.

Строки и столбцы матрицы соответствуют элементам множества X. Элементы матрицы принимают значение, равное степени принадлежности элементов множества X2 множеству 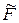 .
.
в) Графический способ. Графически нечеткое отношение может быть задано в виде ориентированного взвешенного графа (рис. 8.10), где вес ребра соответствует значению степени принадлежности элемента множеству 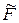 .
.

Рис. 8.10. График отношения 
Пример 8.8. Заданы нечеткие отношения 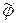 = (X,
= (X, 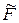 ) (рис. 8.10) и
) (рис. 8.10) и  = (X,
= (X,  ) (рис. 8.11)Найти их объединение, пересечение и композицию.
) (рис. 8.11)Найти их объединение, пересечение и композицию.

Рис. 8.11. График отношения 
Ответ:
а) Объединение (рис. 8.12).
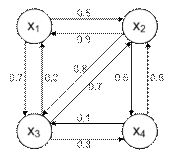
Рис. 8.12. Результат объединения отношений 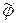 и
и 
б) Пересечение (рис. 8.13).
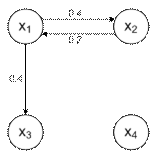
Рис. 8.13. Результат пересечения отношений  и
и 
в) Композиция (рис. 8.14).

Рис. 8.14. Результат композиции отношений  и
и 
Для работы с нечеткостями используется также теория приближенных множеств, разработанная З. Павлаком. Основное преимущество этой теории, что при работе с ней не требуется предварительных сведений о степени принадлежности элемента множеству (как в нечетких множествах) и т.п. Использование этой теории помогает исследовать и анализировать неточные знания. Они определяются приближенно в рамках заданного обучающего множества на основе понятий нижнего и верхнего приближений. Причем нижние приближения включают те элементы исходного множества, которые наверняка принадлежат понятию. Верхние приближения включают все элементы исходного множества, которые возможно принадлежат понятию. Промежуточные элементы между этими приближениями образуют граничную область. Она содержит элементы исходного множества, которые не могут быть классифицированы точно на основе исходных данных.
Пусть на обучающем множестве X введено отношение эквивалентности j = < Ф, X >, Ф Í X ´ X. Здесь Ф – график отношения, X – область задания отношения. Упорядоченную пару Q = <j, X > называют пространством приближений. Множество А = { Q1, Q2,…, Ql },будем считать приближенным множеством.
Классы эквивалентности по отношению к j называют элементарными множествами в кортеже Q. Составным множеством в Q считается конечное объединение элементарных множеств в Q. Следуя Вагину В.Н. и др., все множество классов эквивалентности обозначим j*(D) = { e 1, e 2, …, en }, где D – множество атрибутов.
Пустое множество является также элементарным для любого пространства приближений. Любое конечное объединение элементарных множеств в Q называется составным множеством.
Под нижним приближением множества X в Q будем понимать наибольшее составное множество в Q, содержащееся в X, а под верхним приближением X в Q — наименьшее составное множество в Q, содержащее X. Обозначим нижнее и верхнее приближения множества X в пространстве Q через  Х и
Х и  X соответственно. Множество Впр (Х) =
X соответственно. Множество Впр (Х) =  X -
X -  Х будем называть границей X в Q.
Х будем называть границей X в Q.
Рассмотрим пример. Пусть задана следующая таблица 8.1.
Таблица 8.1
| Фамилия | Сфера деятельности | Уровень доходов |
| Иванов | Управление | Высокий |
| Петрова | Торговля | Средний |
| Сидоров | Производство | Средний |
| Николаев | Наука | Низкий |
| Попова | Управление | Высокий |
Положим D = {Сфера деятельности}, тогда обучающая выборка разбивается на четыре класса эквивалентности:
R *(D) ={{Иванов, Попова}, {Петрова}, {Сидоров}, {Николаев}}.
Здесь е 1 = {Иванов, Попова}, е 2 = {Петрова}, е 3 = {Сидоров}, е 4 = {Николаев}.
Любое объединение элементарных множеств называется составным множеством. Так, множество { е 2, е 3} = {Петрова, Сидоров} - составное множество.
Пусть в нашем примере X — класс людей с высоким доходом. Тогда
 Х = {Иванов, Попова}
Х = {Иванов, Попова}
 Х = {Иванов, Попова, Петрова, Сидоров}
Х = {Иванов, Попова, Петрова, Сидоров}
ВпР (Х) =  X -
X -  Х ={Петрова, Сидоров}.
Х ={Петрова, Сидоров}.
Приближенные множества в основном используются для классификации объектов.
Два произвольных множества Y и Z приближенно равны снизу в Р, если равны их нижние приближения в пространстве Р:  Y =
Y =  Z.
Z.
Множества Y и Z приближенно равны сверху, если совпадают их верхние приближения:  Y =
Y =  Z.
Z.
Если два множества приближенно равны сверху и снизу одновременно, они называются приближенно равными и обозначаются как Y» Z.
Для приближенных множеств справедливы следующие выражения:
1.  Y Ì Y Ì
Y Ì Y Ì  Y
Y
2.  1 =
1 =  l = 1
l = 1
3.  0 =
0 =  0 = 0
0 = 0
4.  (Y Ç Z) =
(Y Ç Z) =  Y Ç
Y Ç  Z
Z
5.  (Y È Z) =
(Y È Z) =  Y È
Y È  Z
Z
6.  Y = -
Y = -  (- Y)
(- Y)
7.  Y = -
Y = -  (- Y)
(- Y)
Здесь 0 обозначает пустое множество, 1 обозначает все множество X.
Контрольные вопросы
1. Что такое нечеткое множество?
2. Привести способы задания нечеткого множества.
3. Что называется нечетким высказыванием? Привести примеры нечетких высказываний.
4. Как определяется степень истинности сложного нечеткого высказывания?
5. Как определяется степень включения двух нечетких множеств?
6. Как определяется операция дополнения нечеткого множества?
7. Как определяются операции объединения, пересечения, разности двух или более нечетких множеств?
8. Что называется нечетким соответствием?
9. Как определяются операции инверсии и композиции для нечетких соответствий?
10. Что называется нечетким отношением?
11. Как определяются операции над нечеткими отношениями?
12. Что такое приближенное множество?
13. Привести способы задания приближенного множества.
14. Приведите примеры приближенных множеств.
Задания для самостоятельной работы
1. Пусть задано произвольное четкое множество X = {0, 1, 2,..., 10}. Задать нечеткие множества, соответствующие, по вашему мнению, понятиям “не много”, ”не мало”, ”средне”, ”очень мало”, ”очень много”, ”вполне достаточно”, ”не много и не мало”, ”не очень много и не очень мало”.
2. Пусть  ,
,  ,
,  - нечеткие высказывания, причем
- нечеткие высказывания, причем  = 0.3,
= 0.3,  = 0.8,
= 0.8,  = 0.1.
= 0.1.
Определить степень истинности составного высказывания  , если:
, если:
a)  = (
= ( ®
®  ) ®
) ®  ;
;
б)  = (ù
= (ù  Ú ù
Ú ù  ) & ù
) & ù  ;
;
в)  = (ù
= (ù  ®
®  ) Ú ù
) Ú ù  ;
;
г)  = ù((ù
= ù((ù  «ù
«ù  ) & (ù
) & (ù  ® ù
® ù  ));
));
д)  = ù((
= ù(( Ú ù
Ú ù  ) ®
) ®  ) &
) &  ;
;
е)  = (ù(ù
= (ù(ù  Ú
Ú  ) & ù(
) & ù( Ú ù
Ú ù  ) Ú (
) Ú (  & ù
& ù  )) ®
)) ®  &
&  &
&  ;
;
3. Пусть заданы произвольные нечеткие множества:
 = {<0.8; x1>; <0.4; x2>; <0.3; x3>; <0.6; x4>};
= {<0.8; x1>; <0.4; x2>; <0.3; x3>; <0.6; x4>};
 = {<0.7; x2>; <0.6; x3>; <0.2; x4>; <0.1; x5>}
= {<0.7; x2>; <0.6; x3>; <0.2; x4>; <0.1; x5>}
на произвольном четком множестве X = {x1, x2, x3, x4, x5}.
Найдите нечеткое множество  , такое что:
, такое что:
а)  =
=  Ç
Ç  ;
;
б)  = ù
= ù  Ç
Ç  ;
;
в)  = ù(ù
= ù(ù  Ç ù
Ç ù  );
);
г)  =
=  È
È  ;
;
д)  =
=  È ù
È ù  ;
;
е)  = ù(ù
= ù(ù  È
È  );
);
ж)  =
=  \
\  ;
;
з)  = ù
= ù  \ ù
\ ù  ;
;
и)  = ù(
= ù( \ ù
\ ù  ).
).
4. Пусть задано нечеткое соответствие  = (X, Y,
= (X, Y, 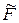 ), где X = {x1, x2, x3, x4}, Y = {y1, y2, y3, y4, y5},
), где X = {x1, x2, x3, x4}, Y = {y1, y2, y3, y4, y5}, 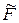 = {<0.7,<x1, y2>>, <0.9,<x1, y5>>, <0.1,<x2, y1>>, <0.3,<x2, y2>>, <0.6,<x2, y3>>, <1,<x3, y4>>, <0.8,<x4, y2>>, <0.4,<x4, y3>>}.
= {<0.7,<x1, y2>>, <0.9,<x1, y5>>, <0.1,<x2, y1>>, <0.3,<x2, y2>>, <0.6,<x2, y3>>, <1,<x3, y4>>, <0.8,<x4, y2>>, <0.4,<x4, y3>>}.
Запишите матрицу инциденций RG, постройте граф соответствия  .
.
5. Для нечетких соответствий  = (X, Y,
= (X, Y, 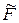 ) и
) и  = (Y, Z,
= (Y, Z,  ), где X = {x1, x2, x3, x4}, Y = {y1, y2, y3, y4, y5},
), где X = {x1, x2, x3, x4}, Y = {y1, y2, y3, y4, y5}, 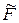 = {<0.7, <x1, y2>>; <0.9, <x1, y5>>; <0.1, <x5, y1>>; <0.3, <x2, y2>>; <0.6, <x2, y3>>; <1, <x3, y4>>; <0.8, <x4, y2>>; <0.4, <x4, y3>>}, Y = {y1, y2, y3, y4}, Z = {z1, z2, z3},
= {<0.7, <x1, y2>>; <0.9, <x1, y5>>; <0.1, <x5, y1>>; <0.3, <x2, y2>>; <0.6, <x2, y3>>; <1, <x3, y4>>; <0.8, <x4, y2>>; <0.4, <x4, y3>>}, Y = {y1, y2, y3, y4}, Z = {z1, z2, z3},  = {<0.6, <y1, z1>>; <0.3, <y1, z2>>; <1, <y3, z3>>; <0.8, <y4, z1>>}. Найти:
= {<0.6, <y1, z1>>; <0.3, <y1, z2>>; <1, <y3, z3>>; <0.8, <y4, z1>>}. Найти:
а)  -1;
-1;
б)  -1;
-1;
в)  °
°  ;
;
г)  -1 °
-1 °  -1.
-1.
6. Заданы нечеткие отношения 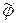 = (X,
= (X, 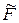 ) и
) и  = (X,
= (X,  ), где X = {x1, x2, x3, x4, x5},
), где X = {x1, x2, x3, x4, x5}, 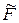 = {<0.4, <x1, x2>>; <0.3, <x1, x3>>; <0.5, <x1, x5>>; <0.9, <x2, x1>>; <0.8, <x2, x3>>; <0.1, <x3, x2>>; <0.6, <x3, x3>>; <0.7, <x5, x1>>; <0.2, <x5, x2>>},
= {<0.4, <x1, x2>>; <0.3, <x1, x3>>; <0.5, <x1, x5>>; <0.9, <x2, x1>>; <0.8, <x2, x3>>; <0.1, <x3, x2>>; <0.6, <x3, x3>>; <0.7, <x5, x1>>; <0.2, <x5, x2>>},  = {<0.3, <x1, x1>>; <0.9, <x1, x4>>; <0.1, <x2, x3>>; <0.4, <x3, x1>>; <0.5, <x4, x2>>}.
= {<0.3, <x1, x1>>; <0.9, <x1, x4>>; <0.1, <x2, x3>>; <0.4, <x3, x1>>; <0.5, <x4, x2>>}.
Найти их пересечение, объединение, инверсию и композицию.
7. На основе данных о прогнозе погоды на неделю (взять из интернета) построить примеры приближенных множеств для следующих действий:
a) путешествия;
b) занятия спортом на открытом воздухе;
c) строительство;
d) остаться дома.
Тестовые задания к модулю 1
1. Объект, принадлежащий множеству, называется его …
· Элементом
· Подмножеством
· Мощностью
· Семейством
· Надмножеством
2. Запись ù("x Î X) (x Î Y) означает:
· Любой элемент x, принадлежащий множеству X, принадлежит и множеству Y
· Существует элемент x, принадлежащий множеству X, являющийся элементом множества Y
· Ни один элемент множества X не принадлежит множеству Y
· Существует элемент x, который принадлежит множеству X и не принадлежит множеству Y
· Не каждый элемент из множества X принадлежит множеству Y
3. Количество элементов конечного множества называется…
· Элементом
· Подмножеством
· Мощностью
· Семейством
· Любой из перечисленных вариантов
Дата добавления: 2015-10-26; просмотров: 595 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Между множествами натуральных чисел и точек сегмента [0, 1] нельзя установить взаимно-однозначное соответствие. | | | Множество A, любой элемент которого принадлежит множеству B, называется… множества B. |