
|
Читайте также: |
Наиболее наглядным способом перехода к совершенным нормальным формам являются карты Карно. Ниже представлены карты Карно для двух, трех и четырех переменных соответственно:

Рис. 13.1. Карты Карно
Как видно, карты Карно составляются таким образом, чтобы значение переменных в соседних клетках отличались друг от друга не более чем на единицу.
Алгоритм перехода к СДНФ можно сформулировать следующим образом:
1. Для заданной функции строится карта Карно.
2. В клетках соответствующих компонентам, составляющим ДНФ, ставятся единицы.
3. Затем для каждой клетки, имеющей единицу, записываются конъюнкции, содержащие полный набор переменных.
4. Полученные конъюнкции соединяются символами дизъюнкции.
Для получения с помощью карт Карно СКНФ необходимо проинвертировать исходную БФ.
Затем для полученного инверсного выражения выполняется алгоритм, приведенный для записи СДНФ.
Полученную в пункте 4 вышеуказанного алгоритма СДНФ еще раз инвертируем и получаем в результате искомую СКНФ.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 13.3. Преобразовать в СДНФ и СКНФ следующие переключательные функции:
а) Y = А В Ú С.
Решение. Как видно, исходная функция имеет две составляющие, соединенные между собой символом дизъюнкции. Используя законы и тождества алгебры логики, преобразуем эти составляющие до полных. Согласно тождествам алгебры логики, значение выражения типа В Ú  всегда равно единице, поэтому добавление такого выражения в исходное не изменяет его значения. Применив к полученному выражению распределительный закон, перейдем к записи СДНФ:
всегда равно единице, поэтому добавление такого выражения в исходное не изменяет его значения. Применив к полученному выражению распределительный закон, перейдем к записи СДНФ:
А В (С Ú  ) = А В С Ú А В
) = А В С Ú А В  ;
;
С (А Ú  ) = С А Ú С
) = С А Ú С  = (С А Ú С
= (С А Ú С  ) (В Ú
) (В Ú  ) = А В С Ú
) = А В С Ú  В С Ú А
В С Ú А  С Ú
С Ú 
 С.
С.
Ответ: YСДНФ = А В С Ú А В  Ú
Ú  В С Ú А
В С Ú А  С Ú
С Ú 
 С.
С.
б) Y = А (В Ú  ).
).
Решение. Исходная функция состоит из двух составляющих, соединенных символом конъюнкции. Для того, чтобы записать исходную функцию в виде СКНФ, необходимо, чтобы каждая составляющая включала в себя полный набор переменных, соединенных знаком конъюнкции. Согласно тождествам алгебры логики значение выражения типа В  всегда равно нулю, поэтому добавление такого выражения в исходное не изменяет его значения. Применив после этого к полученному выражению распределительный закон, мы легко перейдем к записи СКНФ:
всегда равно нулю, поэтому добавление такого выражения в исходное не изменяет его значения. Применив после этого к полученному выражению распределительный закон, мы легко перейдем к записи СКНФ:
А = А Ú В  = (А Ú В) (А Ú
= (А Ú В) (А Ú  ) = (А Ú В Ú С
) = (А Ú В Ú С  ) Ú (А Ú
) Ú (А Ú  Ú С
Ú С  ) = (А Ú В Ú С) (А Ú В Ú
) = (А Ú В Ú С) (А Ú В Ú  ) (А Ú
) (А Ú  Ú С) (А Ú
Ú С) (А Ú  Ú
Ú  );
);
В Ú С = В Ú C Ú А  = (А Ú В Ú C) (
= (А Ú В Ú C) ( Ú В Ú С).
Ú В Ú С).
Ответ. YСКНФ = (А Ú В Ú С) (А Ú В Ú  ) (А Ú
) (А Ú  Ú С) (А Ú
Ú С) (А Ú  Ú
Ú  ) (
) ( Ú В Ú С).
Ú В Ú С).
в) Y = А ( Ú С) (
Ú С) ( Ú В Ú С);
Ú В Ú С);
Решение. А = А Ú В  = (А Ú В) (А Ú
= (А Ú В) (А Ú  ) = (А Ú В Ú С
) = (А Ú В Ú С  ) Ú (А Ú
) Ú (А Ú  Ú С
Ú С  ) = (А Ú В Ú С) (А Ú В Ú
) = (А Ú В Ú С) (А Ú В Ú  ) (А Ú
) (А Ú  Ú С) (А Ú
Ú С) (А Ú  Ú
Ú  );
);
 Ú C =
Ú C =  Ú C Ú А
Ú C Ú А  = (А Ú
= (А Ú  Ú С) (
Ú С) ( Ú
Ú  Ú С);
Ú С);
Ответ. YСКНФ = (А Ú В Ú С) (А Ú В Ú  ) (А Ú
) (А Ú  Ú С) (А Ú
Ú С) (А Ú  Ú
Ú  ) (
) ( Ú
Ú  Ú С).
Ú С).
г) Y = А Ú  С Ú
С Ú  В С;
В С;
Решение.  С (А Ú
С (А Ú  ) = А
) = А  С Ú
С Ú 
 С;
С;
А (С Ú  ) = С А Ú
) = С А Ú  А = (С А Ú
А = (С А Ú  А) (В Ú
А) (В Ú  ) = А В С Ú А В
) = А В С Ú А В  Ú А
Ú А  С Ú А
С Ú А 
 .
.
Ответ. Yсднф = А В С Ú А В  Ú А
Ú А  С Ú А
С Ú А 
 Ú
Ú 
 С.
С.
Пример 13.4. Преобразовать с помощью карт Карно переключательную функцию:
а) Y = А В Ú С в СДНФ.
Решение. Исходная функция содержит две составляющие А В и С. Строим карту Карно. Конъюнкция А В соответствует столбцу 11в карте Карно. Проставляем единицы во всех ячейках этого столбца. Вторая составляющая С исходной функции соответствует строке 1 в карте Карно. Во всех ячейках данной строки также проставляем единицы. В результате этой операции мы получили карту Карно, изображенную ниже.
| С\АВ | ||||
Данная карта имеет пять ячеек, содержащих единицы. Следовательно, СДНФ исходной функции должна содержать пять конъюнкций. Запишем теперь исходную функцию в совершенной дизъюктивной нормальной форме:
Yсднф = А В С Ú А В  Ú
Ú  В С Ú А
В С Ú А  С Ú
С Ú 
 С.
С.
б) Y = (А Ú В Ú С) (А Ú  Ú D) в СКНФ.
Ú D) в СКНФ.
Решение. Найдем инверсное значение функции Y:
 =
= 

 Ú
Ú  В
В 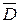 .
.
Построим карту Карно аналогично описанному в предыдущем примере способу.
| СD\AB | ||||
Полученная карта Карно содержит четыре ненулевых ячейки. После этого запишем выражение, являющееся инверсией СКНФ.
 =
= 


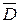 Ú
Ú 

 D Ú
D Ú  В
В 
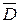 Ú
Ú  В С
В С 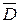 .
.
Теперь, для того чтобы получить СКНФ, достаточно проинвертировать последнее выражение:
YСКНФ = (А Ú В Ú С Ú D) (А Ú В Ú С Ú 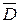 ) (A Ú
) (A Ú  Ú C Ú D) (
Ú C Ú D) ( Ú B Ú C Ú
Ú B Ú C Ú 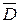 ).
).
13.3. Алгебра Жегалкина
Другая алгебра булевых функций строится на основе операций сложения по модулю 2 и конъюнкции. Она называется алгеброй Жегалкина (АЖ).
Свойства АЖ:
1) Коммутативность x Å y = y Å x, xy = yx.
2) Ассоциативность x Å(y Å z) = (x Å y)Å z, x (y z) = (x y) z.
3) Дистрибутивность умножения относительно сложения x (y Å z) = x y Å x z.
4) Свойства констант x 1 = x, x 0 = 0, x Å0 = x.
Справедливы также соотношения:
 = 1Å x, x 1 Ú x 2 = x 1Å x 2Å x 1 x 2, x 1Å x 2 = x1
= 1Å x, x 1 Ú x 2 = x 1Å x 2Å x 1 x 2, x 1Å x 2 = x1  Ú
Ú  x 2.
x 2.
Используя эти формулы, можно перейти от АЖ к БА и обратно.
Например.
1) x ( Ú y) = x [(1Å x)Å y Å(1Å x) y ] = x (1Å x Å y Å y Ú x y) = x (1Å x Å x y) = x Å x x Å x x y = x y.
Ú y) = x [(1Å x)Å y Å(1Å x) y ] = x (1Å x Å y Å y Ú x y) = x (1Å x Å x y) = x Å x x Å x x y = x y.
2) 1Å x Å y Å x y = (1Å x)(1Å y) = 
 .
.
Через операции алгебры Жегалкина можно выразить все другие БФ. Пример показан в табл. 13.2.
Таблица 13.2.
x 1 ® x 2 =  Ú x 2 = 1Å x 1Å x 1 x 2 Ú x 2 = 1Å x 1Å x 1 x 2
|
x 1 ~ x 2 = ( Ú x 2)(x 1 Ú Ú x 2)(x 1 Ú  ) = 1Å x 1Å x 2 ) = 1Å x 1Å x 2
|
x 1 x 2 =  = x 1Å x 1 x 2 = x 1Å x 1 x 2
|
x 1 | x 2 = 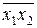 = 1Å x 1 x 2 = 1Å x 1 x 2
|
x 1 ¯ x 2 =  = 1Å x 1Å x 2Å x 1 x 2 = 1Å x 1Å x 2Å x 1 x 2
|
13.4. Функциональная полнота БФ
В алгебре логики из множества n =  различных БФ n переменных y = f (x 1,..., xn) выделяют пять типов БФ.
различных БФ n переменных y = f (x 1,..., xn) выделяют пять типов БФ.
1) Функции, сохраняющие константу 0, т.е. такие f (x 1,..., xn), что f (0,..., 0) = 0, их число  .
.
2) Функции, сохраняющие константу 1, т.е. такие f (x 1,..., xn), что f (1,..., 1) = 1, их число равно половине общего числа всех функций n переменных т.е.  .
.
3) Самодвойственные функции, т.е. такие, которые, принимают противоположные значения на любых двух противоположных наборах. Их число  .
.
4) Линейные функции, т.е. такие, которые представляются в алгебре Жегалкина каноническим многочленом, не содержащим произведений переменных a 0 + a 1 x 1 +... + anxn, где коэффициенты a 0,..., an принимают значения 0 или 1. Так как всего коэффициентов n + 1, то число различных линейных функций будет  .
.
5) Монотонные функции, т.е. такие, которые для любых двух наборов из множества значений переменных, частично упорядоченного соотношением (a 1,..., an) £ (b 1,..., bn), при ai £ bi (i = 1, 2,..., n), удовлетворяют неравенству f (a 1,..., an) £ f (b 1,..., bn).
Система функций, суперпозицией которых представляется любая функция из некоторого множества БФ, называется функционально полной. Если в такой системе допускаются константы 0 и 1, то ее называют ослаблено функционально полной. Говорят, что ФПС функций образует базис в логическом пространстве. Система функций называется минимально полным базисом, если удаление из нее любой функции превращает эту систему в неполную.
Дата добавления: 2015-10-26; просмотров: 138 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Для выбора «лучшего» алгоритма необходимо получение оценок или границ для объема памяти и времени работы ЭВМ, которое потребуется алгоритму для обработки конкретных данных. 4 страница | | | Теорема о функциональной полноте |