
Читайте также:
|
Подставляем в рассматриваемое высказывание значения логических переменных и получаем выражение:
0 Ú 1 Ú 0 Ù 0 ® 1.
Как видно, одна из дизъюнкций составляющих данное выражение содержит единицу, следовательно, все выражение истинно и мы можем на этом остановиться. Таким образом, можно сказать, что исходное высказывание истинно.
Пример 12.2. Для составного логического высказывания, заданного в примере 1, определить такой набор значений логических переменных x, y, z, при котором значение составного высказывания было бы ложно.
Решение: Поскольку в исходном высказывании имеется операция дизъюнкции, то для того, чтобы это высказывание было ложным, необходимо, чтобы одновременно были ложны высказывания: x Ù ( Ú
Ú  Ú z Ù y ®
Ú z Ù y ®  ) и
) и  Ù y. Рассмотрим эти высказывания по отдельности, причем поскольку второе высказывание содержит меньше переменных, начнем именно с него. Очевидно, что для того, чтобы было ложно высказывание
Ù y. Рассмотрим эти высказывания по отдельности, причем поскольку второе высказывание содержит меньше переменных, начнем именно с него. Очевидно, что для того, чтобы было ложно высказывание  Ù y, необходимо, чтобы либо
Ù y, необходимо, чтобы либо  , либо y, либо обе переменные одновременно были ложны. Таким образом, с учетом инверсии переменной x получили три возможных набора значений переменных x и y:
, либо y, либо обе переменные одновременно были ложны. Таким образом, с учетом инверсии переменной x получили три возможных набора значений переменных x и y:
(x = 1, y = 1; x = 1, y = 0; x = 0, y = 0).
Теперь рассмотрим вторую составляющую:
x Ù ( Ú
Ú  Ú z Ù y ®
Ú z Ù y ®  ).
).
Для этого будем поочередно подставлять полученные ранее наборы в составное высказывание, заключенное в скобки.
Возьмем первый набор: x = 1, y = 1. Поскольку х истинно, то значение высказывания в скобках должно быть ложным. Подставив значения x и y в высказывание в скобках, получим:
0 Ú 0 Ú z Ù 1 ®  .
.
Это выражение может быть ложно в двух случаях. Во-первых, если переменная равна нулю, в таком случае вне зависимости от результата импликации данное выражение будет ложно. А во-вторых, оно будет ложно, если будет ложным результат импликации. Как известно, операция импликации ложна только в случае, если левая половина импликации истинна, а правая - ложна. Из данного высказывания видно, что результат импликации будет ложным в случае, если z = 1.
Таким образом, мы получили два набора значений переменных, при котором исходное высказывание ложно: х = 1, y = 1, z = 1; х = 1, y = 1, z = 0.
Проанализировав аналогичным образом остальные варианты, получим еще два набора логических переменных, при которых исходное высказывание ложно:
1) x = 0, y = 0, z = 0;
2) x = 0, y = 0, z = 1.
Ответ. Полученный результат можно записать в виде таблицы истинности (см. табл. 12.1) логической функцииY:
Y = x Ù ( Ú
Ú  Ú z Ù y ®
Ú z Ù y ®  ) Ú
) Ú  Ù y.
Ù y.
Таблица 12.1
| x | y | z | Y |
12.2. Основные логические тождества и законы
Приведем основные тождества и законы Булевой алгебры.
Переместительный закон (коммутативность):
x Ú y = y Ú x; x Ù y = y Ù x. (1.1)
Сочетательный закон (ассоциативность):
(x Ú y) Ú z = x Ú (y Ú z) = x Ú y Ú z;
(x Ù y) Ù z = x Ù (y Ù z) = x Ù y Ù z. (1.2)
Распределительный закон (дистрибутивность):
x Ú (y Ù z) = (x Ú y) Ù (x Ú z); x Ù (y Ú z) = (x Ù y) Ú (x Ù z).(1.3)
Закон Де Моргана:
 =
= 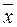 Ù
Ù  ;
; 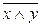 =
=  Ú
Ú  . (1.4)
. (1.4)
Закон двойного отрицания:
 = х. (1.5)
= х. (1.5)
Закон повторяемости:
х Ú х = х; х Ù х = х. (1.6)
Тождества:
x Ú 0 = x; x Ú 1 = 1; x Ú 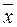 = 1;
= 1;
x Ù 0 = 0; x Ù 1 = x; x Ù  = 0. (1.7)
= 0. (1.7)
Правила поглощения:
x Ú (x Ù y) = x; x Ù (x Ú y) = x. (1.8)
Правила склеивания: 
(x Ù y) Ú (x Ù  ) = x; (x Ú y) Ù (x Ú
) = x; (x Ú y) Ù (x Ú  ) = x. (1.9)
) = x. (1.9)
Следствия из закона Де Моргана:
x Ú y = 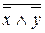 ; x Ù y =
; x Ù y =  . (1.10)
. (1.10)
Тождества:
x ® y =  Ú y, (1.11)
Ú y, (1.11)
x ® y =  ®
®  , (1.12)
, (1.12)
(x ® y) Ù (y ® x) = x «y, (1.13)
 ® y =
® y =  ® x = x Ú y. (1.14)
® x = x Ú y. (1.14)
Справедливость всех вышеуказанных законов и тождеств доказывается с помощью таблиц истинности.
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Пример 12.3. Доказать с помощью таблиц истинности справедливость распределительного закона:
(А Ú В) Ù C = А Ù С Ú В Ù С.
Решение. Для доказательства справедливости данного закона приведем таблицы истинности для каждой из частей тождества:
Таблица 12.2
| А | В | С | А Ú В = Р1 | Р1 Ù С = Q1 |
Как видно из табл. 12.2, сначала записываются все возможные наборы значений переменных A, B, C. Так как в рассматриваемом примере имеется три переменных, то существует восемь различных вариантов таких наборов. Затем последовательно выполняются все необходимые логические операциидля каждого такого набора. Так, например, в четвертом столбце табл. 1.2 отражен результат промежуточной операции дизъюнкции между переменными A и B. Пятый столбец табл. 1.2 представляет собой результат выполнения логических операций, описанных левой частью исходного выражения. Аналогичное действие производится и для правой части исходного логического выражения.
Таблица 12.3
| А | В | С | А Ù С = Р1 | В Ù С = Р2 | Р1 Ú Р2 = Q2 |
Сравнив итоговые выражения Q1 и Q2в табл. 12.2.и12.3, можно увидеть, что они совпадают, Q1 = Q2, и, следовательно, исходное тождество справедливо.
Пример 12.4. Доказать с помощью законов и тождеств алгебры логики равенство функций X1 и X2, где:
X1 =  В С Ú А
В С Ú А  С Ú А В
С Ú А В  Ú А
Ú А 
 Ú
Ú  В
В  Ú А В С;
Ú А В С;
X2 = А  Ú В.
Ú В.
Примечание: Здесь и далее для краткости будем использовать запись А В вместо записи А Ù В.
Решение. Минимизируем выражение X1. Для этого сгруппируем конъюнкции таким образом, чтобы конъюнкции одной группы отличались друг от друга только на одну составляющую, например:
( В С Ú
В С Ú  В
В  ) Ú (А
) Ú (А  С Ú А
С Ú А 
 ) Ú (А В
) Ú (А В  Ú А В С).
Ú А В С).
Теперь выносим за скобки одинаковые составляющие:
( В (С Ú
В (С Ú  )) Ú (А
)) Ú (А  (С Ú
(С Ú  )) Ú (А В (С Ú
)) Ú (А В (С Ú  )).
)).
Так как согласно тождествам алгебры логики: С Ú  = 1, то функцию X1 можно записать в следующем виде:
= 1, то функцию X1 можно записать в следующем виде:
X1 =  В Ú А
В Ú А  Ú А В.
Ú А В.
Продолжаем группировать составляющие функцию X1 высказывания. После группировки  В и А В получим:
В и А В получим:
 В Ú А В = В (
В Ú А В = В ( Ú А) = В.
Ú А) = В.
Таким образом, мы пришли к выражению: X1 = А  Ú В.
Ú В.
Следовательно, X1 = X2, что и требовалось доказать.
12.3. Булевы функции одной и двух переменных
Для представления функций используются таблицы истинности.
Областью определения БФ от n переменных служит множество слов длины n. Они представляют собой все возможные наборы из n двоичных цифр и их общее количество n =  . При n = 3 число возможных наборов
. При n = 3 число возможных наборов  = 256, а при n = 5 число наборов
= 256, а при n = 5 число наборов  > 4 миллиардов. В табл.12.4 представлена БФ одной переменной:
> 4 миллиардов. В табл.12.4 представлена БФ одной переменной:
Таблица 12.4
| Y | x 0 1 | Обозначение | Название |
| y 0 | 0 0 | const 0 | |
| y 1 | 0 1 | x | переменная x |
| y 2 | 1 0 | 
| инверсия x |
| y 3 | 1 1 | const 1 |
Функции y 0 = 0 и y 3 = 1 — функции константы (тождественный нуль и тождественная единица).
Приведем таблицу булевых функций для двух переменных (табл. 12.5).
Таблица 12.5
| Y | x 1 0011 x 2 0101 | СДНФ СКНФ | Обозна-чение | Название |
| y 0 |
(x 1 Ú x 2)(x 1 Ú  )( )( Ú x 2)( Ú x 2)( Ú Ú  ) )
| const 0 | ||
| y 1 | x 1 x 2
(x 1 Ú x 2)(x 1 Ú  )( )( Ú x 2) Ú x 2)
| x 1 x 2 | конъюнкция | |
| y 2 | x 1  (x 1 Ú x 2)(x 1 Ú
(x 1 Ú x 2)(x 1 Ú  )( )( Ú Ú  ) )
| x 1 x 2 | Отрицание импликации | |
| y 3 | x 1  Ú x 1 x 2
(x 1 Ú x 2)(x 1 Ú Ú x 1 x 2
(x 1 Ú x 2)(x 1 Ú  ) )
| x 1 | переменная x 1 | |
| y 4 |  x 2
(x 1 Ú x 2)( x 2
(x 1 Ú x 2)( Ú x 2)( Ú x 2)( Ú Ú  ) )
| x 2 x 1 | Отрицание обратной импликации | |
| y 5 |  x 2 Ú x 1 x 2
(x 1 Ú x 2)( x 2 Ú x 1 x 2
(x 1 Ú x 2)( Ú x 2) Ú x 2)
| x 2 | переменная x 2 | |
| y 6 |  x 2 Ú x 1 x 2 Ú x 1  (x 1 Ú x 2)(
(x 1 Ú x 2)( Ú Ú  ) )
| x 1 Å x 2 | неравнознач-ность | |
| y 7 |  x 2 Ú x 1 x 2 Ú x 1  Ú x 1 x 2
(x 1 Ú x 2) Ú x 1 x 2
(x 1 Ú x 2)
| x 1 Ú x 2 | дизъюнкция | |
| y 8 |   (x 1 Ú
(x 1 Ú  )( )( Ú x 2)( Ú x 2)( Ú Ú  ) )
| x 1 ¯ x 2 | Стрелка Пирса | |
| y 9 |   Ú x 1 x 2
(x 1 Ú Ú x 1 x 2
(x 1 Ú  )( )( Ú x 2) Ú x 2)
| x 1 ~ x 2 | Эквивалент-ность | |
| y 10 |   Ú x 1 Ú x 1  (x 1 Ú
(x 1 Ú  )( )( Ú Ú  ) )
| 
| Инверсия x 2 | |
| y 11 |   Ú x 1 Ú x 1  Ú x 1 x 2
(x 1 Ú Ú x 1 x 2
(x 1 Ú  ) )
| x 2 ® x 1 | Обратная импликация | |
| y 12 |   Ú Ú  x 2
( x 2
( Ú x 2)( Ú x 2)( Ú Ú  ) )
| 
| Инверсия x 1 | |
| y 13 |   Ú Ú  x 2 Ú x 1 x 2
( x 2 Ú x 1 x 2
( Ú x 2) Ú x 2)
| x 1 ® x 2 | Импликация | |
| y 14 |   Ú Ú  x 2 Ú x 1 x 2 Ú x 1  (
( Ú Ú  ) )
| x 1 ½ x 2 | Штрих Шеффера | |
| y 15 |   Ú Ú  x 2 Ú x 1 x 2 Ú x 1  Ú x 1 x 2 Ú x 1 x 2
| const 1 |
Как видно, в табл. 12.5 встречаются некоторые неизвестные ранее понятия. Опишем их.
Стрелка Пирса - приводится к виду  и называется операцией ИЛИ - НЕ.
и называется операцией ИЛИ - НЕ.
Штрих Шеффера - можно привести к виду  и называется операцией И - НЕ.
и называется операцией И - НЕ.
Функцииотрицания импликации (прямой и обратной) называются иначе функциями запрета по х 1 и х 2 соответственно и читаются (не х 2, а х 1) и наоборот.
Всякая функция от меньшего числа переменных содержится среди функций большего числа переменных. Между функциями имеются зависимости, на основании которых можно записать соотношения для констант 0 =  и 1 =
и 1 =  , для функции одной переменной х =
, для функции одной переменной х =  и для функций двух переменных: x 1 x 2 =
и для функций двух переменных: x 1 x 2 =  ,
,  =
=  , x 1 Ú x 2 =
, x 1 Ú x 2 =  .
.
Дата добавления: 2015-10-26; просмотров: 189 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Для выбора «лучшего» алгоритма необходимо получение оценок или границ для объема памяти и времени работы ЭВМ, которое потребуется алгоритму для обработки конкретных данных. 1 страница | | | Для выбора «лучшего» алгоритма необходимо получение оценок или границ для объема памяти и времени работы ЭВМ, которое потребуется алгоритму для обработки конкретных данных. 3 страница |