Поверхности B-spline: Алгоритм de Boor

Так как вы уже знаете алгоритм de Casteljau для поверхностей Безье, то алгоритм de Boor для поверхностей B-spline и его модификация для поверхностей NURBS - это чуть-чуть посложнее. Фактически, принимая во внимание свойство локального изменения, алгоритм de Boor выглядит очень похожим на алгоритм de Casteljau. Если уравнение поверхности B-spline переписать следующим образом:

,

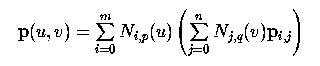то для фиксированного i, выражение для кривой в скобках - это просто кривая B-spline, определяемая контр. точками ряда i. Чтобы упростить наше рассуждение, примем (ага, и закусим:) - прим. перев.)

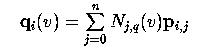
Таким образом, q _i (v) - это точка, соответствующая v на кривой B-spline, определяемой точками на i -м ряду. Если v лежит на узловом интервале [ v_d, v_{d +1}), то только q +1 контр. точек на ряду i участвуют в вычислении q _i (v), где q - это степень N_j,q (v). Эти контр. точки - это p _i,d, p _{i,d -1},..., p _i,d-q, если v не равно v_d. В другом случае, если v равно v_d, узлу множественности t, то участвующие точки - это p _i,d-t, p _{i,d-t -1},..., p _i,d-q. Таким образом, используя контр. точки с столбца d-q по столбец d-t, где t равно нулю, если v - это не узел, мы можем применить алгоритм de Boor к каждому ряду, чтобы получить m +1 новых точек q ₀(v), q ₁(v),..., q _m (v). Это показано на следующей схеме.

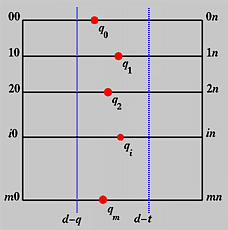
Подставляя эти новые точки обратно в уравнение поверхности, получим следующее

Таким образом, p (u, v) - это точка на кривой B-spline, определяемой точками q ₀(v), q ₁(v),..., q _m (v). В итоге, чтобы найти p (u, v), все, что нужно сделать - это найти точку на кривой, которая соответствует u. Отсюда, алгоритм de Boor снова подходит для этой цели.

Пусть u лежит на узловом интервале [ u_c, u_{c +1}). По свойству локального изменения, только p +1 контр. точек будут участвовать в вычислениях, где p - это степень кривой B-spline. Таким образом, если u не равно u_c, то зависимые точки - это q _c (v), q _{c -1}(v),...., q _c-p (v). В другом случае, если u равно u_c, узлу множественности s, зависящие точки - это q _c-s (v), q _{c-s -1}(v),..., q _c-p (v). Основываясь на этом наблюдении, хоть из каждого ряда получается q _i (v), не все они нужны. Фактически, нужен только p +1 ряд. Это показывает следующая схема:

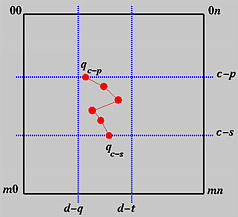
В итоге, если дано u на [ u_c, u_{c +1}) и v на [ v_d, v_{d +1}), p (u, v), для ряда i в пределах между c-p и c-s, применение алгоритма de Boor к контр. точкам p _i,d-q, p _{i,d-q +1},..., p _i,d-t дает новую точку q _i (v). Затем, применяя алгоритм de Boor к q _c-p (v), q _{c-p +1}(v),..., q _c-s (v) и результат - это p (u, v)!

В итоге, получаем следующее:

Вход: набор m +1 рядов и n +1 столбцов контр. точек, узловые векторы в направлениях u и v и значение (u, v);
Выход: точка p (u, v) на поверхности
Алгоритм:

Пусть u лежит на [ u_c, u_{c +1});
Пусть v лежит на [ v_d, v_{d +1});
Если u не равно u_c, примем s равным нулю; иначе s будет множественностью u_c;
Если v не равно v_d, примем t равным нулю; иначе t будет множественностью v_d;
for i:= c-p to c-s do

Begin

Применяем алгоритм de Boor к контр. точкам p _i,d-q, p _{i,d-q +1},..., p _i,d-t относительно v;
Пусит результат будет q _i (v);

End

Применяем алгоритм de Boor к точкам q _c-p (v), q _{c-p +1}(v),..., q _c-s (v) относительно u;
Полученная точка - это p (u, v);

Следующий рисунок иллюстрирует пример. Это поверхность B-spline, определяемая 5×5 контрю точками и узловым вектором (в обоих направлениях) { 0, 0, 0, 0, 0.5, 1, 1, 1, 1 }. Таким образом, степень кривой в обоих направлениях равна 3.

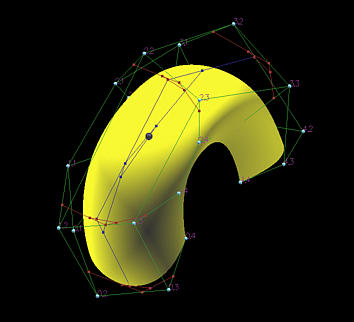
На этом рисунке ни u, ни v не являются узлами, а u меньше 0.5, так как v больше 0.5. Для этого v, так как оно лежит на [0.5, 1), только контр. точки p _{i ,1}, p _{i ,2}, p _{i ,3} и p _{i ,4} участвуют в расчете по алгоритму de Boor. Так как u лежит на [0,0.5), то в направлении u используются только ряды 0, 1, 2 и 3. На рисунке красные ломаные нужны для вычисления значений q _i (v), а единственная синяя ломаная - для вычисления точки на поверхности.

Выбор Параметров: Обзор [Parameter Selection Overview]

Входными данными для алгоритма интерполяции/аппроксимации B-spline обычно является набор точек. Таким образом, первый шаг заключается в том, чтобы найти набор параметров, который бы "фиксировал" эти точки в определенных значениях. Говоря точнее, если данные точки - это d ₀,..., d _n, то нужно найти n +1 параметров t ₀,..., t_n на области определения кривой, чтобы данная точка d _k соответствовала параметру t_k для k между 0 и n. Это значит, что, если p (u) - это кривая, проходящая через все данные точки в определенном порядке, то имеем d _k = p (t_k) для всех 0 <= k <= n. На рисунке ниже, семь исходных точек (т.e. n = 6) и семь параметров, которые нужно найти, чтобы получить искомое.

Есть бесконечное количество вариантов выбора этих параметров. Например, можно разделить пополам область кривой или случайным образом выбрать n +1 значений на области. Тем не менее, плохо выбранные параметры могут привести к неожиданным результатам. Следующий рисунок показывает четыре исходных точки и три интерполированных кривых, каждая из которых получена по своему набору параметров. Одна из них сильно выгибается наружу и получается ненужная выпуклость. Только одна из них достаточно точно следует по направлению исходных точек.

Таким образом, выбор параметров влияет на форму кривой, и, как следствие, влияет на параметризацию кривой.

На нескольких следующих страницах мы обсудим несколько методов выбора параметров, включая Метод Равномерного Распределения [Uniformly Spaced Method], Метод Длины Хорды [Chord Length Method] и Центростремительный Метод [Centripetal Method]. Получив набор параметров, нужно вычислить узловой вектор. Подробности смотрите в Получение Узлового Вектора [Knot Vector Generation] Также обсудим Универсальный Метод [Universal Method], в котором выбирается равномерно разделенный узловой вектор и затем с его помощью находятся параметры Пожалуйста, имейте в виду, что есть еще и другие методы выбора параметров.

Дата добавления: 2015-10-29