Поверхности Безье: Алгоритм de Casteljau

Алгоритм de Casteljau можно расширить и для случая поверхностей. Говоря точнее, можно применить алгоритм de Casteljau несколько раз для того, чтобы найти соответствующую точку на поверхности Безье p (u, v) для данного (u, v). Эта страница описывает это расширение алгоритма, основываясь на понятии изопараметрических кривых, рассмотренном на предыдущей странице.

Вспомним, что уравнение поверхности Безье

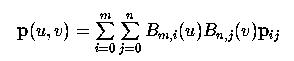
можно переписать в следующем виде

Для i = 0, 1,..., m, определим q _i (v) следующим образом:

Для фиксированного v, имеем m +1 точек q ₀(v), q ₁(v),..., q _m (v). Каждое q _i (v) - это точка на кривой Безье, определяемой контр. точками p _{i 0}, p _{i 1},..., p _in. Подставляя эти значения обратно в уравнение поверхности, получим

Это значит, что p (u, v) - это точка кривой Безье, определяемая m +1 контр. точками q ₀(v), q ₁(v),..., q _m (v). Таким образом, приходим к следующему выводу:

Чтобы найти точку p(u, v) на поверхности Безье, мы можем найти m +1 точек q₀(v), q₁(v),..., q _m (v) и затем из этих точек получить p(u, v).

Этот вывод дает нам простой способ вычисления p (u, v) для данных (u, v). И вот почему. Так как каждое q _i (v) - это точка на кривой Безье, определяемой i -м рядом контр. точек: p _{i 0}, p _{i 1},..., p _in. Таким образом, для i -го ряда и данного v, мы можем применить алгоритм de Casteljau для кривой Безье, чтобы вычислить q _i (v). После m +1 применений алгоритма de Casteljau (т.e. по разу на каждый ряд), мы получим q ₀(v), q ₁(v),..., q _m (v). Затем, снова применяя алгоритм de Casteljau к этим m +1 контр. точкам для u, получим итоговую точку p (u, v) на поверхности!

Следующая схема иллюстрирует это понятие. Данная поверхность - это поверхность Безье степени (2,2), определяемая контрольной сеткой 3x3. Пусть u = 2/3, а v = 1/3. Чтобы определить q ₀(1/3), берем 0-й ряд контр. точек p ₀₀, p ₀₁ и p ₀₂ и применяем алгоритм de Casteljau к этой кривой Безье для v = 1/3. Повторяем это с первым и вторым рядом для v = 1/3. Отсюда получим три промежуточные точки q ₀(1/3), q ₁(1/3) и q ₂(1/3). Наконец, применяем алгоритм de Casteljau к этим трем новым точкам при u = 2/3. Результат - точка p (2/3,1/3), показана на рисунке желтым.

Далее показан пример нахождения точки с изображенной поверхностью Безье. Контр. точки показаны белым. В этой контрольной сетке четыре ряда и пять столбцов и поэтому степень поверхности - (3,4). Для каждого ряда, промежуточные ломаные, используемые в алгоритме de Casteljau, показаны красным. Четыре промежуточных контр. точки q ₀, q ₁, q ₂ и q ₃ также показаны на рисунке. Промежуточные ломаные для этого применения алгоритма de Casteljau показаны синим, а конечная точка p (u, v) на поверхности показана темной сферой.

В итоге, алгоритм сводится к следующему:

Вход: a m +1 рядов и n +1 столбцов контр. точек и (u, v).
Выход: точка на поверхности p (u, v)
Алгоритм:

for i:= 0 to m do

Begin

Применяем алгоритм de Casteljau к i -му ряду контр. точек по v;
Пусть полученная точка будет q _i (v);

End

Применяем алгоритм de Casteljau к q ₀(v), q ₁(v),..., q _m (v) по u;
Полученная точка -это p (u, v);

Дата добавления: 2015-10-29