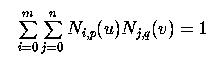Поверхности B-spline: Важные Свойства

Здесь перечисляются некоторые важные свойства поверхностей B-spline. Эти свойства можно легко проверить, используя те же методы, что и для кривых B-spline. Пожалуйста, сравните эти важные свойства со свойствами кривых B-spline. Вспомним уравнение поверхности B-spline:

,

где степени в направлениях u и v равны p и q, и есть m +1 рядов и n +1 столбцов контр. точек.

• Неотрицательность: N_i,p (u) N_j,q (v) неотрицательно для всех p, q, i, j и u и v в пределах от 0 до 1.
  Это очевидно.
• Деление Единства: Сумма всех N_i,p (u) N_j,q (v) равна 1 для всех u и v в пределах от 0 до 1.
  Говоря точнее, это значит, что для любой пары чисел u и v в пределах от 0 до 1, выполняется следующее:

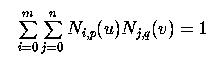
• Свойство Сильного Огранич. Многоугольника: если (u, v) лежит на [ u_i, u_{i +1}) x [ v_j, v_{j +1}), то p(u, v) лежит в огранич. многоугольнике контр. точек p _h,k, где i-p <= h <= i и j-q <= k <= j.
  Это свойство для поверхностей B-spline следует прямо из свойства сильноог огранич. многоугольника для кривых B-spline. Для направления u, если u лежит на [ u_i, u_{i +1}), то существует самое большее p +1 ненулевых базисных функций, а именно N_i,p (u), N_{i -1, p} (u),..., и N_i-p,p (u). Таким образом, только контр. точки на рядах с i-p -го по i -й имеют ненулевые базисные функции в направлении u. Аналогично, если v лежит на [ v_j, v_{j +1}), то существует самое большее q +1 ненулевых базисных функций на этом узловом интервале, а именно N_j,q (v), N_{j -1, q} (v),..., и N_j-q,q (v). Таким образом, только контр. точки на столбцах с j-q -го по j -й имеют ненулевые базисные функции в направлении v. Объединяя два этих факта, получаем, что только контр. точки в пределах от ряда i-p до ряда i и от столбца j-q до столбца q имеют ненулевые базисные функции. Так как эти базисные функции неотрицательны и их сумма равна единице (свойство деления единства), то p (u, v) лежит в огранич. многоугольнике этих контр. точек.

В итоге, элемент поверхности, определенный на прямоугольнике [ u_i, u_{i +1}) x [ v_j, v_{j +1}), лежит полностью в том же огранич. многоугольнике.

• Схема Локального Изменения: N_i,p (u) N_j,q (v) равно нулю, если (u, v) находится снаружи прямоугольника [ u_i, u_{i+p +1}) x [ v_j, v_{j+q +1})
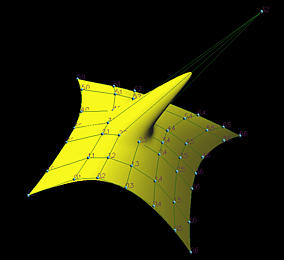
  Из свойства схемы локального изменения мы знаем, что в направлении u N_i,p (u) не равно нулю на [ u_i, u_{i+p +1}), а в остальных случаях равно нулю. Схема локального изменения для поверхностей B-spline идет прямо от того же свойства кривых. Если контр. точка p _3,2 перемещается в новое положение, это показано на следующих рисунках, то только область вокруг этой точки изменяется, а вся остальная поверхность остается неизменной.

Дата добавления: 2015-10-29