Параметрические Поверхности

Параметрические поверхности, или, точнее, участки параметрических поверхностей, не используются по отдельности. Обычно, много таких участков объединяют вместе сторона к стороне, чтобы получить более сложную форму. Следующий рисунок показывает четыре участка поверхностей, объединенных вместе для получения в итоге большей по площади области:

Для того, чтобы вычислить касательный и нормальный векторы в точке (u, v) на области определения, нам нужны частные производные. Пусть параметрическая поверхность определяется так:

Частные производные по u и v - это касательные векторы в точке f (u, v):

На картинке слева - касательный вектор в направлении u, а справа - касательный вектор в направлении v. Нормальный вектор в f (u, v), n (u, v), равен векторному произведению этих частных производных по правилу правой руки:

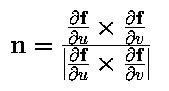
Участок параметрической поверхности можно считать объединением (бесконечного числа) кривых. Есть много способов составления таких объединений кривых; но самый простой способ - так называемые изопараметрические [isoparametric] кривые. Дана параметрическая поверхность f (u, v), если u сделать фиксированной, скажем, 0.1, и изменять v, то получим кривую на поверхности, координата u которой постоянна. Это изопараметрическая кривая в направлении v для u = 0.1. Соответственно, приняв v постоянным, равным какому-то значению, и изменяя u, получим изопараметрическую криву, у которой направление v постоянно. Таким образом, принимая u фиксированным в 0, 0.1, 0.1,..., 0.9 и 1, мы получим 11 изопараметрических кривых f (0, v), f (0.1, v), f (0.2, v),..., f (0.9, v) и f (1, v). Эти кривые развертываются в поверхность, если изменять u от 0 до 1 непрерывно. Аналогично, параметрические кривые, полученные при непрерывном изменении v дадут поверхность. Следующий рисунок показывает несколько изопараметрических кривых в обоих направлениях.

Эти изопараметрические кривые могут помочь в расчете поверхности. Во многих приложениях параметрическая поверхность делится на треугольники или полигоны. Затем эти треугольники и полигоны можно эффективно расчитать с помощью существующих графических библиотек, таких как OpenGL или PHIGS PLUS.

Вместо разделения поверхности на треугольники может быть проще разделить на треугольники область определения (u, v). Мы можем разделить u -направление на m сегментов точками u ₀=0, u ₁,..., u_i,..., u_m =1 и разделить v -направление на n сегментов точками v ₀=0, v ₁,..., v_j,..., u_n =1. Область делится на m ×n прямоугольников, каждый из которых, в свою очередь, можно поделить на два треугольника.

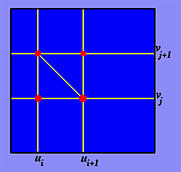
Пусть u_i и u_{i +1} - это две последовательные разделительные точки в направлении u, а v_j и v_{j +1} - в направлении v, как показано выше. Имеем прямоугольник с вершинами (u_i, v_j), (u_{i +1}, v_j), (u_{i +1}, v_{j +1}) и (u_i, v_{j +1}). Есть два способа разделить его на трегольники, так как у него две диагонали. Сделаем, как показано на рисунке. Первый треугольник определяется точками (u_i, v_j), (u_{i +1}, v_j) и (u_i, v_{j +1}), а второй треугольник - точками (u_{i +1}, v_j), (u_{i +1}, v_{j +1}) и (u_i, v_{j +1}).

Возьмем треугольник, определяемый точками (u_i, v_j), (u_{i +1}, v_j) и (u_i, v_{j +1}). Эти три точки переходят в три точки на поверхности f (u_i, v_j), f (u_{i +1}, v_j) и f (u_i, v_{j +1}) с нормальными векторами n (u_i, v_j), n (u_{i +1}, v_j) и n (u_i, v_{j +1}). Теперь у нас есть три грани, у каждой из которых есть нормальный вектор. Этих трех частей информации достаточно для получения гладкого треугольника [to render the triangle smoothly]. В результате у нас есть метод для получения параметрической поверхности. Или, если хотите, у нас есть метод для получения набора треугольников, который приближается к форме данной параметрической поверхности. Эта аппроксимация не очень хороша, так как может получить очень большое количество треугольников, а некоторые из них могут быть в неправильных местоположениях, или, например, слишком маленькими. Эту ситуацию может исправить техника "адаптации". С помощью этого метода динамически изменяются размеры, количество и положения треугольников.

Дата добавления: 2015-10-29