Параметры и Узловые Векторы для Поверхностей

Поверхность B-spline степени (p, q), определяемая e +1 рядами и f +1 столбцами контр. точек имеет следующее уравнение

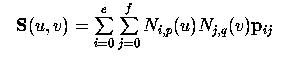
Для него нужны два набора параметров для интерполяции и аппроксимации поверхности. Допустим, у нас есть m +1 ряда и n +1 столбца исходных точек d _ij, где 0 <= i <= m и 0 <= j <= n. Таким образом, нужны m +1 параметров s ₀,..., s_m в направлении u (т.e. по одному на каждый ряд исходных точек) и n +1 параметров t ₀,..., t_n в направлении v (т.e. по одному на каждый столбец исходных точек), чтобы точка (s_c, t_d) на области определения поверхности соответствовала точке S (s_c, t_d) на поверхности, которая, в свою очередь, соответствовала исходной точке d _cd. Представляя это в виде уравнения, точка на поверхности в (s_c, t_d), как показано ниже

,

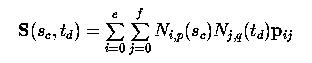соответствует исходной точке d _cd, где s_c и t_d - это параметры в направлениях u и v, соответственно.

В уравнении желаемой поверхности B-spline направление u соответствует индексу i в N_i,p (u) и p _ij. Так как i пробегает от 0 до m, то N _{0, p} (u), N _{1, p} (u),..., N_m,p (u) - это коэффициенты столбцов контр. точек. Таким образом, в направлении u, нам нужно m +1 параметров, и с помощью метода вычисления параметров, использующего степень p и исходные точки из столбца j, мы можем вычислить m +1 параметров u _{0, j}, u _{1, j},..., u_m,j. Это показано на рисунке ниже. Желаемые параметры s ₀, s ₁,..., s_m просто являются средними значениями каждого ряда. Говоря точнее, параметр s_i - это среднее из параметров ряда i, s_i = (u_{i ,0} + u_{i ,1} +... + u_i,n)/(n +1).

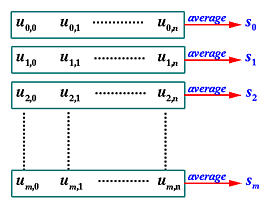
Аналогично вычисление параметров в направлении v. В каждом ряду n +1 исходных точек, поэтому нужно n +1 параметров. Таким образом, для исходных точек ряда i, мы можем вычислить n +1 значений параметров v_{i ,0}, v_{i ,1},..., v_i,n. Так как всего m +1 рядов, то эти значения можно сгруппировать в матрицу (m +1)×(n +1), и тогда параметр t_j - это просто среднее из параметров столбца j, t_j = (v _{0, j} + v _{1, j} +... + v_m,j)/(m +1). Таким образом, мы получаем n +1 параметров в направлении v.

Эта процедура выглядит следующим образом:

Вход: (m +1)×(n +1) исходных точек d _i,j; Выход: Параметры в направлении u s ₀,..., s_m и параметры в направлении v t ₀,..., t_n; Алгоритм: /* вычисляем s ₀,..., s_m */ for j:= 0 to n do /* столбец j */ Находим набор из m +1 параметров u _{0, j}, u _{1, j},..., u_m,j; for i:= 0 to m do s_i = (u_{i ,0} + u_{i ,1} +... + u_i,n)/(n +1); /* параметры для направления u найдены */ /* вычисляем t ₀,..., t_n */ for i:= 0 to m do /* ряд i */ Находим набор из n +1 параметров v_{i ,0}, v_{i ,1},..., v_i,n; for j:= 0 to n do t_j = (v _{0, j} + v _{1, j} +... + v_n,j)/(m +1); /* параметры для направления v найдены */

Затем, значения параметров s ₀, s ₁,..., s_m и степень p вместе определяют узловой вектор U в направлении u. Аналогично, параметры t ₀, t ₁,..., t_n и степень q вместе определяют узловой вектор V в направлении v. Нажмите тут, чтобы посмотреть способ вычисления узлового вектора из набора параметров.

Заметьте, что вышеизложенный алгоритм только показывает принцип вычислений и является неэффективным. Так как теперь вы знаете, что делать, то переделать алгоритм, чтобы он был более эффективным, не составит для вас особого труда. Заметьте, этот алгоритм работает только для методов равномерного распределения, длины хорды и центростремительного метода. Для универсального метода, из-за того, что исходные точки не участвуют в вычислении, мы можем применить равномерные узлы к одному ряду и одному столбцу исходных точек для вычисления параметров.

Дата добавления: 2015-10-29