Нахождение Решения

Пусть желаемая интерполированная кривая B-spline степени p следующая:

Эта кривая B-spline имеет n + 1 неизвестных контр. точек. Так как параметр t_k соответствует исходной точке d _k, то, подставляя t_k в вышеуказанное уравнение, получим следующее:

Так как в вышеуказанном уравнении n + 1 базисных функций B-spline (т.e. N _{0, p} (u), N _{1, p} (u), N _{2, p} (u),... и N_n,p (u), и n + 1 параметр (т.e. t ₀, t ₁, t ₂,... и t_n), то, подставив эти t_k в N_i,p (u) получим (n +1)² значений. Эти значения можно записать в виде матрицы N размера (n +1)×(n +1), в которой k -й ряд содержит значения N _{0, p} (u), N _{1, p} (u), N _{2, p} (u),... и N_i,p (u) для t_k, как показано ниже:

Давайте также соберем векторы d _k и p _i в дае матрицы D и P следующим образом:

Здесь будем считать, что исходная точка d _k является вектором в s -мерном пространстве (т.e. d _k = [ d_{k 1},..., d_ks ]) и стоит в k -м ряду матрицы D. Аналогично, считаем p _i вектором в s -мерном пространстве (т.e. p _i = [ p_{i 1},..., p_is ]) и что она находится в i -м ряду матрицы P. Заметьте, что в трехмерном пространстве s = 3, а на плоскости s = 2. Также заметьте, что матрицы D и P - обе размера (n +1)× s. Затем, нетрудно проверить, что соотношение между значениями d _k и t_i преобразуется к такому более простому виду:

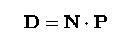
Так как матрица D содержит исходные точки и матрица N получены вычислением базисных функций B-spline по данным параметрам, то D и N - обе известны, а неизвестно только P. Так как это просто система линейных уравнений с неизвестным P, то, решая относительно P, получим контр. точки и желаемая интерполированная кривая B-spline станет доступной. Таким образом, задача интерполяции кривой решена!

Алгоритм

Матрицы D и P - не являются матрицами-столбцами, но это не большая проблема. Можно решать систему по столбцам. Говоря точнее, пусть i -й столбец D и i -й столбец P будут d ⁱ и p ⁱ, соответственно. Из вышеуказанной системы линейных уравнений, получаем следующее:

Затем, решая относит. p ⁱ из N и d ⁱ даст i -й столбец P. Проделываем это для каждого i в пределах от 0 до h, и получим в итоге P. Таким образом, все контр. точки найдены. Как вы, наверное, заметили, это очень неэффективно. К счастью, многие вычислительные библиотеки имеют процедуры решения систем линейных уравнений, которые подходят для эффективного решения уравнения D = N ^. P. Получается, провести кривую B-spline по n +1 точкам не так уж сложно. Оно сводится к решению системы линейных уравнений. Следующий алгоритм объединяет все сказанное:

Вход: n +1 исходных точек d ₀,..... d _n и степень p
Выход: Кривая B-spline степени p, содержащая все эти исходные точки в данном порядке.
Алгоритм:

Выбираем метод для нахождения набора из n +1 параметров t ₀,..., t_n;
Заодно получим и узловой вектор U;
for i:= 0 to n do

for j:= 0 to n do

Вычисляем [Evaluate] N_j,p (t_i) и ставим в ряд i и столбец j матрицы N;

/* матрица N найдена */
for i:= 0 to n do

Помещаем исходную точку d _i в ряд i матрицы D;

/* матрица D построена */
Решаем систему уравнений и находим P из D = N ^. P
Ряд i матрицы P - это контр. точка p _i;
Контр. точки p ₀,..., p _n, узловой вектор U и степень p определяют интерполированную кривую B-spline;

Ниже, на рисунке (а), показан пример. Здесь 9 исходных точек, показаны черным. Найденные контр. точки показаны синим. Маленькие красные точки на интерполированной кривой - это точки, соответствующие узлам, вычисленным по методу длины хорды. В этом случае, эти "узловые точки" находятся довольно близко к исходным точкам и контр. ломаная также проходит близко к исходной, хоть и не всегда. Например, на рисунке (b), исходная и контрольная ломаные очень отличаются.

(a)	(b)

Важно отметить, что матрица N целиком положительна и окружена полосой с половиной ширины меньше [banded with a semi-bandwidth less than] p (т.e. N_i,p (t_k) = 0, если | i - k | >= p), если узлы вычисляются по среднему значению от p последовательных параметров. Это было доказано de Boor в 1978 г. Подробности в Получении Узлового Вектора. Это значит, что система линейных уравнений, полученная по вышеизложенному алгоритму, может быть решена методом исключения Гаусса без вращения [центрирования? pivoting].

Дата добавления: 2015-10-29