Поиск Решения

Этот раздел будет немного непонятным и потребует некоторых знаний в линейной алгебре. Во-первых, давайте перепишем d _k - p (t_k) в другом виде:

Здесь d ₀, d _k и d _n даны, а N _{0, p} (t_k) и N_h,p (t_k) можно найти вычислением N _{0, p} (u) и N_h,p (u) для t_k. Для удобства, определим новый вектор q _k:

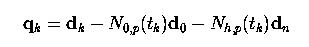
Затем, функцию суммы квадратов f () можно переписать так:

Далее, определим, на что же похож квадрат расстояния погрешности Вспомним тождество x ^. x = | x |². Это значит, что скалярное произведение вектора x на самого себя дает квадрат его длины. Таким образом, квадрат погрешности можно переписать как

Затем, функция f () становится

Как минимизировать эту функцию? Функция f () - это эллиптический параболоид для переменных p ₁,..., p _{h -1}. Таким образом, мы можем продифференцировать f () по каждому p _g и найти нули этих производных. Там, где производная равна нулю, функция достигает экстремума, в данном случае f () достигает минимума.

В вычислении производной по p _g, заметьте, что все q _k и N_i,p (t_k) - это константы (т.e. без участия p _k) и их частные производные по любой p _g должны быть равны нулю. Таким образом, имеем

Возьмем второй элемент из суммы, который является суммой значений N_i,p (t_k) p _i ^. q _k. Производная каждой из его составляющих вычисляется так:

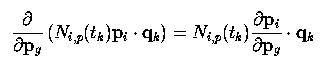
Частная производная p _i по p _g не равна нулю только если i = g. Таким образом, частная производная второго члена суммирования равна:

Производная третьего члена уже сложнее; но все-таки не очень. Здесь испльзуется правило умножения (f^.g)' = f'^.g + f^.g'.

Так как частная производная p _i по p _g равна нулю, если i не равно g, то частная производная третьего члена суммирования по p _g равна:

Объединяя эти результаты, получаем, что частная производная f () по p _g равна

Приравнивая ее к нулю, получим:

Так как имеется h -1 переменных, то g изменяется от 1 до h -1 и всего h -1 таких уравнений. Заметьте, что эти уравнения являются линейными для неизвестных p _i. Перед тем, как продолжить, определим три матрицы:

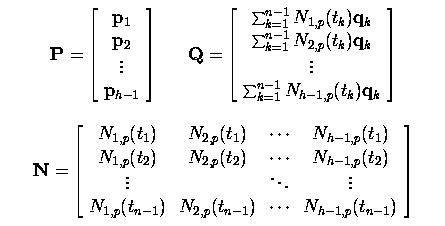
Здесь k -й ряд P - это вектор p _k, k -й ряд Q - это правая сторона k -го уравнения, а k -й ряд N содержит значения вычислений N _{1, p} (u), N _{2, p} (u),..., N_{h -1, p} (u) для t_k. Таким образом, если исходные точки - это s -мерные векторы, то P, N и Q - это матрицы размеров соответственно (h -1)× s, (n -1)×(h -1) и (h -1)× s.

Теперь перепишем g -е линейное уравнение

в другом виде, чтобы коэффициент при p _i легче читался:

Таким образом, коэффициент при p _i равен

Если взглянуть на матрицу N, то видно, что N_g,p (t ₁), N_g,p (t ₂),..., N_g,p (t_{n -1}) - образуют g -й столбец N, а N_i,p (t ₁), N_i,p (t ₂),..., N_i,p (t_{n -1}) - i -й столбец N. Заметьте, что g -й столбец N - это g -й ряд транспонированной матрицы N, N ^T, а коэффициент p _i равен "скалярному" произведению g -го ряда N ^T и i -го столбца N. Имея это ввиду, систему линейных уравнений можно переписать в таком виде

Так как N и Q известны, то решая эту систему линейных уравнений относительно P, получим искомые контр. точки.

Алгоритм

Хоть разработка предыдущего раздела была долгой и нудной, результат удивительно прост: решение системы линейных уравнений примерно как в глобальной интерполяции. В итоге алгоритм для глобальной аппроксимации также довольно простой.

Вход: n +1 исходных точек d ₀, d ₁,..., d _n, степень p, и желаемое количество контр. точек h +1;
Выход: Кривая B-spline степени p, определяемая h +1 контр. точками, которая аппроксимируется к исходным точкам;
Алгоритм:

Получаем набор параметров t ₀,..., t_n и узловой вектор U;
Принимаем p ₀ = d ₀, а p _h = d _n;
for k:= 1 to n -1 do

Вычисляем q _k по следующей формуле:

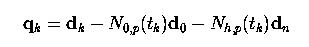
for i:= 1 to h -1 do

Вычисляем следующее и записываем в i -й столбец матрицы Q;

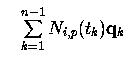
/* матрица Q получена */
for k:= 1 to n -1 do

for i:= 1 to h -1 do

Вычисляем N_i,p (t_k) и записываем в ряд k и столбец i матрицы N;

/* матрица N получена */
Вычисляем M = N ^T. N;
Находим P из M ^. P = Q;
Ряд i матрицы P - это контр. точка p _i;
Контр. точки p ₀,..., p _h, узловой вектор U и степень p определяют аппроксимирующую кривую B-spline;

Дата добавления: 2015-10-29