Системы линейных уравнений (СЛУ).

– система m линейных уравнений с n неизвестными.

– матрица коэффициентов системы.

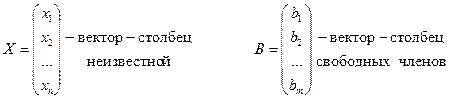
АХ=В – матричная форма записи системы линейных уравнений.

Расширенной матрицей () системы называется матрица коэффициентов системы, дополненная столбцом свободных членов.

Система называется совместной, если она имеет хотя бы одно решение, и несовместной – если ни одного.

Совместная система называется определенной, если она имеет единственной решение, и неопределенной – если множество решений.

Каждое решение неопределенной системы называется частным решением, а их совокупность – общим решением.

Пример:

Общее решение: x 2 = 1 – x 1. Частные решения: x 1 = 0, x 2 = 1; x 1 = 1, x 2 = 0 и т.д.

Однородная система называется система, у которой все свободные члены равны нулю. Однородная система всегда совместна, т.к. имеет нулевое решение (x₁ = x₂ = … = x_n = 0)

Матричный метод решения невырожденной системы линейных уравнений:

Элементарными преобразованиями матрицы будем называть элементарные преобразования над системой ее строк рассматриваемых как векторы. Если одна матрица получается из другой при помощи цепочки строчечных элементарных преобразований, т.е. элементарными преобразованиями над строками, то эти матрицы называются строчно-эквивалентными.

1. Следовательно, любую строку можно умножить на λ 0.

2. К строке можно прибавить другую строку этой матрицы умноженную на λ 0.

Это будут неособенные строчечные элементарные преобразования.

Теорема: перестановка двух строк матрицы есть результат цепочки элементарных преобразований над строками.

Д-во: 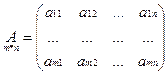рассмотрим т/о две первые строки: 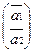+ ~ + ~ 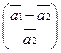+ ~ ~ . Теорема доказана.

Это тоже неособенное строчечно элементарное преобразование.

Рассмотрим вопрос о приведение матрицы к ступенч. виду.

Теорема. Любую матрицу А, m*n можно привести к ступенчатой матрице при помощи цепочки элементарных преобразований над строками.

Пр.

* Столбец матрицы содержащий ведущий элемент строки наз. основным столбцом.

Пр. А= 3-ведущий элемент первой строки; 2-ведущий элемент второй строки; 1 и 2-основные столбцы; 3 и 4-не являются основными столбцами.

Квадратная матрица А называется обратимой матрицей, если квадратная матрица А^-1 такая что, выполняет два условия: 1. А·А^-1=Е; 2. А^-1·А=Е, где Е –единичная матрица.

В этом случае матрица А^-1 наз. обратной матрицей, т. е.

Квадратная матрица А^-1 называется обратной квадратной матрице А, если выполняется два условия 1) А·А^-1=Е; и 2) А^-1·А=Е.

Теорема. (О необратимости):

1) Квадратная матрица с нулевой строкой является необратимой.

2) Квадратная матрица с линейно-зависимыми сроками необратима.

Теорема. (Условия обратимости квадратной матрицы):

Пусть А - кв. м. размерность m*n. Тогда равносильны утверждения:

1) матрица А-обратима,

2) строки матрицы А-линейно-независимы.

3) матрицу А можно представить в виде произвед-я элементарных матриц.

Теорема. Пусть А-квадратная матрица и определитель матрицы |А| 0, тогда: матрица
А-обратима и A^-1= * 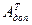(1)

λ 0

получим еще один способ вычисления обратной матрицы.

Теорема. Пусть квадратная матрица А при помощи цепочки неособенных элементарных преобразований над строками можно привести в единичную матрицу Е. Тогда А обратима. Эти же элементарные преобразования переводят Е в матрицу А^-1. Из этой теоремы получаем схему вычисления обратной матрицы: 1) Составим прямоугольную матрицу (). 2) При помощи неособенных элементарных преобразований над строками перевести А в Е, тогда Е допис-й справа перейдет в матрицу А^-1. А~Е, Е~А^-1. (А|Е) ~ (Е|А^-1).

Теорема. Пусть дана СЛУ в матричной форме записи АХ=В (*) и строки матрицы А линейно независимы. Тогда уравнение (*) имеет единственное решение Х=А^-1*В.

Доказательство: 1) докажем что решение:

строки матрицы А линейно независимы => => => 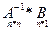. Подставив в уравнение (*) А*Х=А(А^-1*В)= (А*А^-1)*В=В, В=В, верно => =А^-1*В решение.

E

2) докажем единственность: покажем что всякое решение Х имеет вид
А^-1*В. Х=Е*Х= (А^-1*А)*Х=А^-1* (А*Х) А^-1*В, Х=А^-1*В

что и требовалось доказать.

Теорема. Если матрица А обратима, то матрица обратная к ней единственная.

Доказательство: Пусть А обратима, тогда матрица А^-1:

1) А*А^-1=Е,

2) А^-1*А=Е.

Предположим что еще одна матрица С А^-1 и выполняется условие:

3) А*С=Е,

4) С*А=Е.

Тогда А^-1=А^-1*Е А^-1*(А*С) (А^-1*А)*С=Е*С=>А^-1=С.

Получим противоречие, следовательно, наше предположение неверно!

Что и требовалось доказать.

Дата добавления: 2015-10-24