Читайте также:
|
Пусть дано уравнение (1.1), определяющее центральную кривую второго порядка Г.
а) Если 
, то выполним преобразование помощи поворота осей координат на угол 
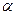, удовлетворяющему условию (1.30). Получим уравнение вида
(1.35)
Коэффициенты уравнения (1.35) связаны с коэффициентами уравнения (1.1) соотношениями (1.29). Приведем уравнение (1.35) к виду
(1.36)
б) Дальнейшее упрощение уравнения (1.36) достигается при помощи преобразования параллельного переноса:
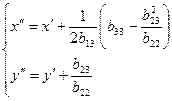(1.37)
В результате получится уравнение вида
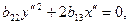(1.38)
соответствующее одному из канонических уравнений 6), 7), 8), 9).
Дата добавления: 2015-07-11; просмотров: 109 | Нарушение авторских прав