Расположение кривой второго порядка

Расположение эллипса или гиперболы относительно начальной системы координат будет известно, если мы будем знать координаты центра и (в случае ) угловой коэффициент большей оси для эллипса и вещественной оси для гиперболы. Координаты центра находятся из системы уравнений (3.1).

Если линия – эллипс и - меньший по абсолютной величине корень характеристического уравнения, то формула

(4.1)

Если уравнение (1.1) определяет гиперболу, и если - корень характеристического уравнения, знак которого совпадает со знаком , то формула

(4.2)

дает угловой коэффициент вещественной оси гиперболы.

Расположение параболы относительно начальной системы координат будет известна, если мы будем знать вершину параболы, вектор, направленный по оси в сторону вогнутости, и параметр. Вершина параболы определяется при решении уравнения оси параболы

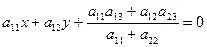
(4.3)

или

(4.3')

совместно с уравнением параболы (2.1). Вектор

(4.4)

параллелен оси параболы и направлен в сторону ее вогнутости.

Параметр параболы определяется по формуле

(4.5)

Дата добавления: 2015-07-11