|
Читайте также: |
Эллиптический параболоид (рис. 3.8), каноническое уравнение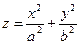 
. Сечения, параллельные оси z, - параболы; сечения параллельные плоскости Oxy – эллипсы. Если a=b, то имеем параболоид, получаемый при вращении параболы 
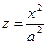, лежащей в плоскости Oxz вокруг её оси.
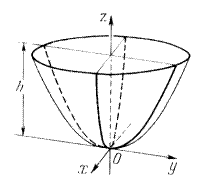Объём части параболоида, отсекаемой плоскостью, перпендикулярной его оси, на высоте h, равен 
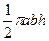, т.е. равен половине объёма эллиптического цилиндра с таким же основанием и высотой.
Рис. 3.8.
Дата добавления: 2015-07-11; просмотров: 724 | Нарушение авторских прав