Читайте также:
|
В зависимости от значения инварианта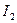 
принята следующая классификация кривых второго порядка. Кривая второго порядка Г, заданная уравнением (2.1), называется центральной, если 
.
Центральная кривая Г называется кривой эллиптического типа, если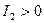 
.
Центральная кривая Г называется кривой гиперболического типа, если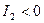 
.
Центром кривой второго порядка Г называется такая точка плоскости, по отношению к которой точки этой кривой расположены симметрично парами. Точка 
является центром кривой второго порядка, определяемой уравнением (2.1), в том и только том случае, когда ее координаты удовлетворяют уравнениям:
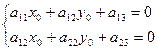(3.1)
Определитель этой системы равен 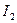. Если , то система имеет единственное решение. В этом случае координаты центра могут быть определены по формулам:
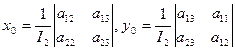(3.2)
В случае 
кривую Г называют кривой параболического типа.
Из теорем 1 и 2 получается следующая классификация кривых второго порядка с помощью инвариантов:
1) эллипс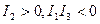 
2) мнимый эллипс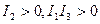 
3) две мнимые пересекающиеся прямые (точка)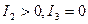 
4) гипербола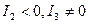 
5) две пересекающиеся прямые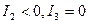 
(3.3)
6) парабола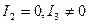 
7) две параллельные прямые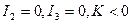 
8) две мнимые параллельные прямые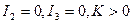 
9) две совпадающие прямые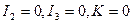 
В прилагаемой схеме приведения кривых второго порядка к каноническому виду для компактности записи коэффициенты уравнения (2.1) переобозначены следующим образом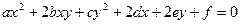 
.
Дата добавления: 2015-07-11; просмотров: 181 | Нарушение авторских прав