Задания для курсовой работы

Задание 1. Дляданного уравнения кривой второго порядка с параметром :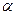

1. С помощью инвариантов определить зависимость типа кривой от .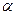

2. При привести данное уравнение кривой к каноническому виду, применяя преобразования параллельного переноса и поворота. Построить кривую в канонической системе координат.

3. При нескольких значениях параметра 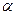построить кривые, определяемые данным уравнением.

Задание 2. Для данного уравнения поверхности второго порядка:

1. Определить тип поверхности (с помощью инвариантов).

2. Привести уравнение к каноническому виду.

3. Исследовать форму поверхности методом сечений.

4. Построить поверхность в канонической системе координат.

Примечания:

1. Структура курсовой работы:

- титульный лист

- оглавление

- задания (постановка задачи)

- выполнение заданий (аналитическая часть и графические иллюстрации)

- выводы (анализ полученных результатов)

- список литературы

- дата и подпись исполнителя

2. Студент обязан выдерживать график выполнения курсовой работы (сроки выполнения отдельных заданий и оформления работы), согласованный с руководителями.

3. Руководителями курсовой могут быть выданы дополнительные задания.

4. При выполнении графической части работы рекомендуется проиллюстрировать все основные случаи.

Например:

а) при выполнении задания 1 следует построить кривые всех возможных типов для данного уравнения с параметром;

б) при исследовании формы поверхности методом сечений в задании 2 следует построить сечения координатными плоскостями и несколькими параллельными им плоскостями.

Варианты:

В1.1. .

2. .

В2. 1. .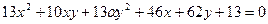

2. .

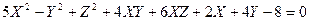В3. 1.

2.

В4. 1.

2.

В5. 1.

2.

В6. 1.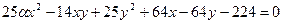

2.

В7. 1.

2.

В8 1.

2.

В9 1.

2.

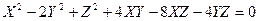
В10 1.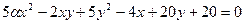

2.

В11 1.

2.

В12 1.

2.

В13 1.

2.

В14 1.

2.

В15 1.

2.

В16 1.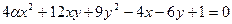

2.

В17 1.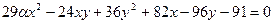

2.

В18 1.

2.

В19 1.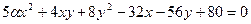

2.

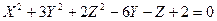
В20 1.

2.

В21 1.

2.

В22 1.

2.

В23 1.

2.

В24. 1.

2.

В25. 1.

2.

В26. 1.

2.

Литература

1. Александров П.С. Лекции по аналитической геометрии. М.: Наука,

2. Беклемешев Д.В. Куpс аналитической геометpии и линейной алгебpы.

М.: Hаука, 1984.

3. Беклемешев Д.В. Дополнительные главы линейной алгебpы. М.: Hаука,

1983.

4. Бугpов Я.С., Hикольский С.М. Элементы линейной алгебpы и

аналитической геометpии. М.: Hаука, 1980.

5. Данко П.Е., Попов А.Г., Кожевникова Т. Я. Высшая математика в упражнениях и задачах. Ч.1.

М: Высшая школа, 1986.

6. Ефимов А.В., Демидович Б.П. Сборник задач по математике для втузов.

Ч.1. М.: Hаука, 1981

7. Ильин В.А., Позняк Э.Г. Аналитическая геометрия. М.: Наука, 1987.

8. Клетеник Д.В. Сборник задач по аналитической геометрии. М.:

Наука, 1974.

9. Моденов П.С. Аналитическая геометрия. М.: Изд-во МГУ,1969

Содержание

1. Кривые второго порядка …………………………………………………………………

1.1 Окружность……………………………………………………………………….

1.2. Эллипс…………………………………………………………………………….

1.3 Гипербола………………………………………………………………………….

1.4 Парабола……………………………………………………………………………

2. Общее уравнение и инварианты кривых второго порядка………………………………

3. Классификация кривых второго порядка…………………………………….………….…

4. Расположение кривой второго порядка………………………………………………………

5. Приведение общего уравнения кривой второго порядка к каноническому виду……….….

6. Схема приведения общего уравнения кривых второго порядка к каноническому виду……

7. Поверхности второго порядка…………………………………………………………………..

7.1 Эллипсоид………………………………………………………………………….……

7.2 Однополосный гиперболоид…………………………………………………….……..

7.3 Двуполостный гиперболоид………………………………………………………..….

7.4 Конус………………………………………………………………………………..…..

7.5 Эллиптический параболоид………………………………………………………..…..

7.6 Гиперболический параболоид………………………………………………………….

7.7 Цилиндры. Параболический цилиндр………………………………………………....

8. Метод сечений на примере исследования формы эллипсоида…………………………….….

9. Общее уравнение и инварианты поверхности второго порядка……………………….….…..

10. Классификация поверхностей второго порядка…………………………………………..…..

Задания для курсовой работы………………………………………………………………….

Литература……………………………………………………………………………………….

Дата добавления: 2015-07-11