
|
Читайте также: |
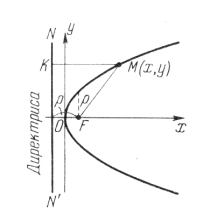
Параболой называется множество точек плоскости, для каждой из которых расстояние до некоторой фиксированной точки, называемой фокусом, равно расстоянию до некоторой прямой,называемой директрисой.
Расстояние от фокуса до директрисы называется параметром параболы и обозначается p.
Пусть точка О расположена посередине между фокусом и директрисой, и ось Ox направлена от О к F. Если d=MK – расстояние от M до директрисы и r =MF, то (рис. 1.7):

 Отсюда
Отсюда 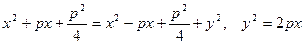 - каноническое уравнение параболы
- каноническое уравнение параболы
Уравнение директрисы: 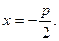
Фокальный радиус точки M: 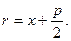
Эксцентриситет параболы считают равным
единице: 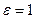 (отметим, что тогда
(отметим, что тогда 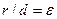 ).
).
Рис. 1.7
Уравнение касательной к параболе 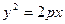 в точке
в точке 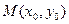
 .
.
Поместим начало полярной системы координат в фокус F параболы 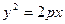 . Так как расстояние от F до директрисы равно p, то полярные координаты (
. Так как расстояние от F до директрисы равно p, то полярные координаты (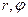 ) произвольной точки
) произвольной точки
М параболы удовлетворяют равенству 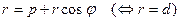 , т.е.
, т.е.
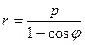 . (1.6)
. (1.6)
Пусть Г – произвольное коническое сечение, F - один из фокусов кривой Г, и пусть S - точка на Г такая, что отрезок FS параллелен директрисе кривой Г. Длину отрезка FS называют фокальным параметром кривой Г и обозначают p. Если 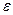 - эксцентриситет кривой Г и d - расстояние от фокуса F до соответствующей директрисы, то
- эксцентриситет кривой Г и d - расстояние от фокуса F до соответствующей директрисы, то 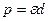 . Аналогично (1.6) в полярной системе координат уравнение
. Аналогично (1.6) в полярной системе координат уравнение
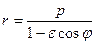
при 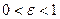 задает эллипс, а при
задает эллипс, а при  одну из ветвей гиперболы.
одну из ветвей гиперболы.
Общее уравнение и инварианты кривых второго порядка
Пусть кривая Г задана в декартовой системе координат 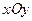 уравнением:
уравнением:
 (2.1)
(2.1)
Если хотя бы один из коэффициентов  отличен от нуля, то кривую Г называют кривой второго порядка.
отличен от нуля, то кривую Г называют кривой второго порядка.
Теорема 1. Для произвольной кривой второго порядка Г существует такая декартова прямоугольная система координат 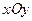 , что в этой системе кривая Г имеет уравнение одного из следующих канонических видов:
, что в этой системе кривая Г имеет уравнение одного из следующих канонических видов:
1)  - эллипс,
- эллипс,
2) 
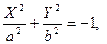 - мнимый эллипс,
- мнимый эллипс,
3) 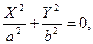 - две мнимые пересекающиеся прямые (точка),
- две мнимые пересекающиеся прямые (точка),
4) 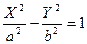 - гипербола
- гипербола
5) 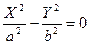 - две пересекающиеся прямые,
- две пересекающиеся прямые,
6) 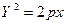 - парабола,
- парабола,
7)  - две параллельные прямые,
- две параллельные прямые,
8) 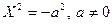 - две мнимые прямые,
- две мнимые прямые,
9) 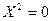 - две совпадающие прямые.
- две совпадающие прямые.
В этих уравнениях 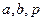 - положительные параметры.
- положительные параметры.
Функция 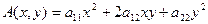 называется квадратичной формой, соответствующей уравнению (2.1). Характеристическим уравнением квадратичной формы
называется квадратичной формой, соответствующей уравнению (2.1). Характеристическим уравнением квадратичной формы 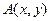 называется уравнение
называется уравнение
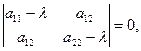 (2.2)
(2.2)
а корни 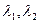 уравнения (2.2) называются характеристическими числами квадратичной формы
уравнения (2.2) называются характеристическими числами квадратичной формы 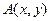 .
.
Характеристическое уравнение (2.2) записывается в виде
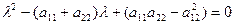 (2.3)
(2.3)
и имеет дискриминант
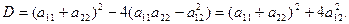 (2.4)
(2.4)
Всегда 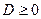 и характеристические числа квадратичной формы
и характеристические числа квадратичной формы 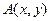 находятся по формуле
находятся по формуле
 (2.5)
(2.5)
В общем случае характеристическое уравнение (2.3) записывается в виде
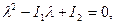 (2.6)
(2.6)
где
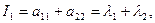 (2.7)
(2.7)
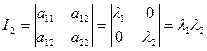 (2.8)
(2.8)
Обозначим
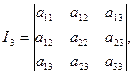 (2.9)
(2.9)
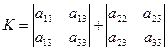 . (2.10)
. (2.10)
Значения 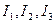 не меняются при переходе от одной декартовой прямоугольной системы координат к другой, полученной в результате поворота осей координат и переноса начала координат, то есть являются инвариантами кривой Г относительно поворота осей координат и переноса начала.
не меняются при переходе от одной декартовой прямоугольной системы координат к другой, полученной в результате поворота осей координат и переноса начала координат, то есть являются инвариантами кривой Г относительно поворота осей координат и переноса начала.
Значение K является инвариантом кривой Г только относительно поворота осей координат.
Теорема 2. Для любой кривой второго порядка Г существует угол 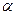 и числа
и числа 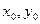 такие, что с помощью преобразования поворота осей и переноса начала координат
такие, что с помощью преобразования поворота осей и переноса начала координат
 (2.11)
(2.11)
уравнение (2.1) приводится к одному из следующих трех видов:
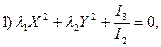 если
если  ; (2.12)
; (2.12)
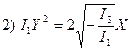 , если
, если  (2.13)
(2.13)
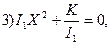 если
если 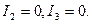 (2.14)
(2.14)
Здесь 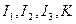 - определены формулами (2.7)-(2.10) соответственно, а
- определены формулами (2.7)-(2.10) соответственно, а 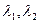 - корни характеристического уравнения (2.6).
- корни характеристического уравнения (2.6).
Для эллипса  - меньший по абсолютной величине корень характеристического уравнения.
- меньший по абсолютной величине корень характеристического уравнения.
Для гиперболы  - корень характеристического уравнения, знак которого совпадает со знаком
- корень характеристического уравнения, знак которого совпадает со знаком  .
.
Дата добавления: 2015-07-11; просмотров: 118 | Нарушение авторских прав