Парабола. В школьном курсе математики достаточно подробно изучалась парабола

В школьном курсе математики достаточно подробно изучалась парабола, которая, по определению, являлась графиком квадратного трехчлена. Здесь мы дадим другое (геометрическое) определение параболы.

Определение. Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до фиксированной точки F этой плоскости, называемой фокусом, равно расстоянию до фиксированной прямой, лежащей в той же плоскости и называемой директрисой параболы.

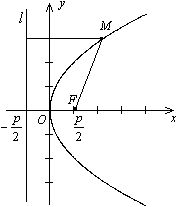
Чтобы получить уравнение кривой, соответствующей этому определению, введем подходящую систему координат. Пусть расстояние между фокусом 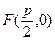и директрисой параболы l, уравнение которой 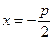, равно p (.

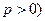Из фокуса F опустим перпендикуляр 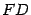на директрису 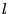(рис. ниже). Начало координат 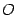расположим на середине отрезка 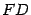, ось 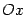направим вдоль отрезка 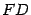так, чтобы ее направление совпадало с направлением вектора . Ось Оу перпендикулярна оси .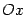

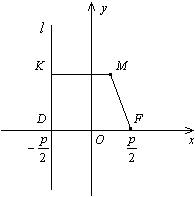
Теорема. В выбранной системе координат парабола имеет уравнение 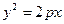(4)

Доказательство. Пусть М (х, у) -- текущая точка параболы. По определению параболы 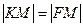. Найдем длины данных отрезков. По формуле для плоского случая находим

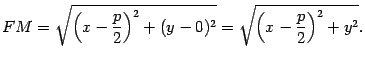
Расстоянием от точки 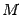до директрисы 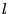служит длина перпендикуляра 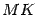, опущенного на директрису из точки 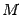. Из рисунка очевидно, что 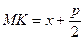. Тогда по определению параболы 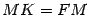, то есть

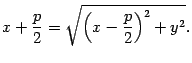
Возведем обе части последнего уравнения в квадрат:

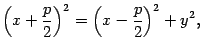
откуда

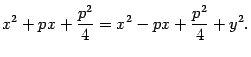
После приведения подобных членов получим уравнение 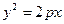(4)

Уравнение (4) называется каноническим уравнением параболы. (что и треб. доказать)

Замечание. Парабола обладает осью симметрии. Если парабола задана каноническим уравнением, то ось симметрии совпадает с осью 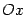. Асимптот парабола не имеет.

Определение. Точка пересечения оси симметрии с параболой называется вершиной параболы.

Построение. Проведем прямую 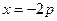. Выберем на ней произвольным образом точку М. Проведем через точку М луч (ОМ) и луч, параллельный оси Ох. Проведем луч, выходящий из начала координат перпендикулярно лучу (ОМ) до пересечения с лучом, параллельным оси Ох. Точка их пересечения принадлежит параболе.

Дата добавления: 2015-07-11