П. 6. Кривые второго порядка.

Определение. Уравнение вида , где А, В, С одновременно не равны нулю, называется общим уравнением кривой второго порядка.

Этому уравнению не всегда соответствует на плоскости множество точек. Если геометрический образ не существует, то есть нет точек, удовлетворяющих уравнению, то говорят, что уравнение определяет мнимую кривую.

Из общего уравнения получаются многочисленные уравнения кривых – канонические уравнения. Ограничимся констатацией того, что уравнение в зависимости от коэффициентов может задавать только четыре типа кривых, а именно, окружность, эллипс, гиперболу и параболу, причем если 1) , то это уравнение эллипса (действительного или мнимого) или точки, в случае А = В – окружность; 2) , то это уравнение гиперболы или двух пересекающихся прямых; 3) , то это уравнение параболы или пары прямых.

Если В = 0, то уравнение называется пятичленным уравнением кривой второго порядка. Приведение такого уравнение к каноническому виду осуществляется путем образования полных квадратов по отношению к переменным х и у: и параллельному переносу начала координат в точку (х ₀, у ₀). Если 1) 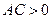, то это уравнение эллипса (действительного или мнимого) или точки; 2) 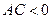, то это уравнение гиперболы или двух пересекающихся прямых; 3) , то это уравнение параболы или пары прямых.

Дата добавления: 2015-07-11