Замечание 1. Другие канонические уравнения параболы.
 .
.


Графики:


Фокусы 

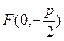
Директриса 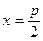

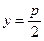
Замечание 2. Есливершина параболы сдвинута и лежит в точке М (х 0, у 0). Тогда ее каноническое уравнение имеет вид:  . Тогда фокус
. Тогда фокус  , уравнение директрисы
, уравнение директрисы 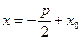 .
.
Парабола так же, как и эллипс, обладает свойством, связанным с отражением света (рис. ниже). Свойство сформулируем опять без доказательства.
Свойство. Пусть  -- фокус параболы,
-- фокус параболы, 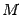 -- произвольная точка параболы,
-- произвольная точка параболы, 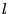 -- луч с началом в точке
-- луч с началом в точке 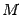 параллельный оси параболы. Тогда нормаль к параболе в точке
параллельный оси параболы. Тогда нормаль к параболе в точке 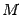 делит угол, образованный отрезком
делит угол, образованный отрезком  и лучом
и лучом 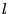 , пополам.
, пополам. 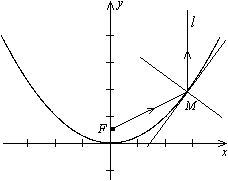
Это свойство означает, что луч света, вышедший из фокуса  , отразившись от параболы, дальше пойдет параллельно оси этой параболы. И наоборот, все лучи, приходящие из бесконечности и параллельные оси параболы, сойдутся в ее фокусе. Это свойство широко используется в технике. В прожекторах обычно ставят зеркало, поверхность которого получается при вращении параболы вокруг ее оси симметрии (параболическое зеркало). Источник света в прожекторах помещают в фокусе параболы. В результате прожектор дает пучок почти параллельных лучей света. Это же свойство используется и в приемных антеннах космической связи и в зеркалах телескопов, которые собирают поток параллельных лучей радиоволн или поток параллельных лучей света и концентрируют его в фокусе зеркала.
, отразившись от параболы, дальше пойдет параллельно оси этой параболы. И наоборот, все лучи, приходящие из бесконечности и параллельные оси параболы, сойдутся в ее фокусе. Это свойство широко используется в технике. В прожекторах обычно ставят зеркало, поверхность которого получается при вращении параболы вокруг ее оси симметрии (параболическое зеркало). Источник света в прожекторах помещают в фокусе параболы. В результате прожектор дает пучок почти параллельных лучей света. Это же свойство используется и в приемных антеннах космической связи и в зеркалах телескопов, которые собирают поток параллельных лучей радиоволн или поток параллельных лучей света и концентрируют его в фокусе зеркала.
Пример 1. Постройте параболу 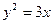 . Найдите ее фокус и директрису.
. Найдите ее фокус и директрису.
Решение. Уравнение является каноническим уравнением параболы, 2 р = 3, р =1,5. Осью параболы служит ось 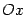 , вершина находится в начале координат, ветви параболы направлены вдоль оси
, вершина находится в начале координат, ветви параболы направлены вдоль оси 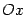 . Для построения найдем несколько точек параболы. Для этого придаем значения переменному у и находим значения
. Для построения найдем несколько точек параболы. Для этого придаем значения переменному у и находим значения  . Возьмем точки
. Возьмем точки 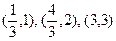 . Учитывая симметрию относительно оси
. Учитывая симметрию относительно оси 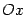 , рисуем кривую (рис.)
, рисуем кривую (рис.)
 Фокус
Фокус  лежит на оси
лежит на оси 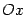 на расстоянии
на расстоянии 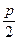 от вершины, то есть имеет координаты (0.75, 0). Директриса
от вершины, то есть имеет координаты (0.75, 0). Директриса 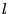 имеет уравнение
имеет уравнение  .
.
Пример 2. Построить параболу  .
.
 Решение. Найдем каноническое уравнение параболы.
Решение. Найдем каноническое уравнение параболы.  , следовательно, вершина параболы в точке М(0, -4), ветви вниз симметрично оси (Оу), 2 р = 1, отсюда
, следовательно, вершина параболы в точке М(0, -4), ветви вниз симметрично оси (Оу), 2 р = 1, отсюда  . Фокус
. Фокус  , уравнение директрисы
, уравнение директрисы 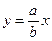 .
.
Дата добавления: 2015-07-11; просмотров: 75 | Нарушение авторских прав
mybiblioteka.su - 2015-2025 год. (0.01 сек.)

 .
.











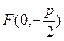
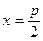

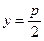
 . Тогда фокус
. Тогда фокус  , уравнение директрисы
, уравнение директрисы 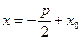 .
. -- фокус параболы,
-- фокус параболы, 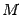 -- произвольная точка параболы,
-- произвольная точка параболы, 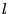 -- луч с началом в точке
-- луч с началом в точке 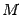 параллельный оси параболы. Тогда нормаль к параболе в точке
параллельный оси параболы. Тогда нормаль к параболе в точке 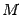 делит угол, образованный отрезком
делит угол, образованный отрезком  и лучом
и лучом 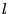 , пополам.
, пополам. 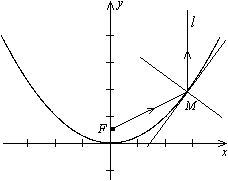
 , отразившись от параболы, дальше пойдет параллельно оси этой параболы. И наоборот, все лучи, приходящие из бесконечности и параллельные оси параболы, сойдутся в ее фокусе. Это свойство широко используется в технике. В прожекторах обычно ставят зеркало, поверхность которого получается при вращении параболы вокруг ее оси симметрии (параболическое зеркало). Источник света в прожекторах помещают в фокусе параболы. В результате прожектор дает пучок почти параллельных лучей света. Это же свойство используется и в приемных антеннах космической связи и в зеркалах телескопов, которые собирают поток параллельных лучей радиоволн или поток параллельных лучей света и концентрируют его в фокусе зеркала.
, отразившись от параболы, дальше пойдет параллельно оси этой параболы. И наоборот, все лучи, приходящие из бесконечности и параллельные оси параболы, сойдутся в ее фокусе. Это свойство широко используется в технике. В прожекторах обычно ставят зеркало, поверхность которого получается при вращении параболы вокруг ее оси симметрии (параболическое зеркало). Источник света в прожекторах помещают в фокусе параболы. В результате прожектор дает пучок почти параллельных лучей света. Это же свойство используется и в приемных антеннах космической связи и в зеркалах телескопов, которые собирают поток параллельных лучей радиоволн или поток параллельных лучей света и концентрируют его в фокусе зеркала. . Найдите ее фокус и директрису.
. Найдите ее фокус и директрису.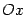 , вершина находится в начале координат, ветви параболы направлены вдоль оси
, вершина находится в начале координат, ветви параболы направлены вдоль оси 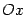 . Для построения найдем несколько точек параболы. Для этого придаем значения переменному у и находим значения
. Для построения найдем несколько точек параболы. Для этого придаем значения переменному у и находим значения  . Возьмем точки
. Возьмем точки 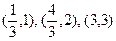 . Учитывая симметрию относительно оси
. Учитывая симметрию относительно оси 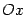 , рисуем кривую (рис.)
, рисуем кривую (рис.) Фокус
Фокус  лежит на оси
лежит на оси 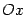 на расстоянии
на расстоянии 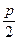 от вершины, то есть имеет координаты (0.75, 0). Директриса
от вершины, то есть имеет координаты (0.75, 0). Директриса 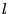 имеет уравнение
имеет уравнение  .
. .
. Решение. Найдем каноническое уравнение параболы.
Решение. Найдем каноническое уравнение параболы.  , следовательно, вершина параболы в точке М(0, -4), ветви вниз симметрично оси (Оу), 2 р = 1, отсюда
, следовательно, вершина параболы в точке М(0, -4), ветви вниз симметрично оси (Оу), 2 р = 1, отсюда  . Фокус
. Фокус  , уравнение директрисы
, уравнение директрисы 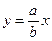 .
.

