
|
Читайте также: |
Определение. Окружностью называется геометрическое место точек плоскости, равноудаленных от фиксированной точки, называемой центром окружности.
Получим уравнение окружности, если известны ее центр и радиус.
Теорема. Окружность радиуса  с центром в точке М 0(х 0, у 0) имеет уравнение
с центром в точке М 0(х 0, у 0) имеет уравнение
 (1) (1)
| 2) |
Доказательство. Пусть М (х, у) -- текущая точка окружности. По определению окружности расстояние ММ 0 равно  , т.е.
, т.е.  , где
, где 


Обе части уравнения неотрицательны. Поэтому после возведения их в
квадрат получим эквивалентное уравнение

Если в данном уравнении раскрыть скобки и привести подобные члены, то вид его изменится. Однако любое уравнение окружности с помощью тождественных преобразований можно привести к каноническому виду (1). Для этого достаточно выделить полные квадраты по переменным  и у.
и у.
Пример. Нарисуйте кривую  .
.
Решение. Сгруппируем  .
.
Выд  елим полные квадраты, получим
елим полные квадраты, получим  .
.
Отсюда  ,
,  .
.
Тогда каноническое уравнение имеет вид:  .
.
Итак, центр окружности – М 0(1,-3), радиус равен 2.
Эллипс
Определение. Эллипсом называется геометрическое место точек плоскости, для каждой из которых сумма расстояний до двух данных точек F 1 и F 2 той же плоскости, назывемых фокусами эллипса, есть величина постоянная и равная 2 а.
 Начало О системы координат расположим на середине отрезка F 1 F 2. Координаты фокусов F 1(-с,0), F 2(с,0). Тогда расстояние между фокусамиравно
Начало О системы координат расположим на середине отрезка F 1 F 2. Координаты фокусов F 1(-с,0), F 2(с,0). Тогда расстояние между фокусамиравно  : | F 1 F 2|=2c.
: | F 1 F 2|=2c.
Ось 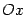 направим вдоль этого отрезка, ось Oy -- перпендикулярно к этому отрезку.
направим вдоль этого отрезка, ось Oy -- перпендикулярно к этому отрезку.
Теорема. В выбранной системе координат эллипс имеет каноническое уравнение
 (2), где
(2), где  или
или 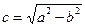
Доказательство. Пусть М (х, у) -- текущая точка эллипса. По определению эллипса F 1 M + F 2 M =2 а. Из треугольника F 1 M F 2 (рис. ниже) видно, что F 1 M + F 2 M > F1F2, то есть 2a > 2c, a > c, и поэтому число  существует.
существует.

Фокусами в выбранной системе координат являются точки F 1(-с,0), F 2(с,0),.
Найдем расстояния F 1 M и F 2 M.

Тогда по определению эллипса

Перенесем один из корней вправо и обе части возведем в квадрат:

После того, как раскроем скобки и приведем подобные члены, приходим к выражению

Разделим обе части этого уравнения на 4 и возведем в квадрат

Раскроем скобку и приведем подобные члены

Учитывая, что  , имеем равенство
, имеем равенство
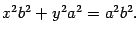
Наконец, разделив обе части на  , получим уравнение
, получим уравнение  . Уравнение называется каноническим уравнением эллипса. (что и треб.доказать).
. Уравнение называется каноническим уравнением эллипса. (что и треб.доказать).
Свойства эллипса: Эллипс обладает двумя взаимно перпендикулярными осями симметрии, на одной из которых находятся его фокусы, и центром симметрии. Если эллипс задан каноническим уравнением), то его осями симметрии служат оси 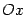 и Оу, начало координат -- центр симметрии.
и Оу, начало координат -- центр симметрии.
Построение эллипса. Строим две окружности с центром в точке О радиусами а и b. (a > b).Строим луч, выходящий из начала координат до пересечения с обеими окружностями. Из точек пересечения опускаем пересекающиеся лучи, параллельные координатным осям. Точка пересечения данных лучей – это очка, принадлежащая эллипсу.
Замечание. Если задано каноническое уравнение эллипса и требуется его построить, то для отображения качественных характеристик достаточно правильно отметить вершины эллипса и провести через них линию, похожую на кривую рис., выдерживая симметрию и избегая образования углов на рисунке. Если же из рисунка предполагается получать числовую информацию о координатах его точек, то тогда построение следует проводить более точно. Нужно построить по точкам верхнюю половину эллипса как график функции  , взяв для построения достаточно много точек, а нижнюю половину эллипса получить, используя его симметрию. С другим способом построения эллипса можно познакомиться в курсе черчения.
, взяв для построения достаточно много точек, а нижнюю половину эллипса получить, используя его симметрию. С другим способом построения эллипса можно познакомиться в курсе черчения.
Определения. Точки пересечения эллипса с его осями симметрии называются вершинами эллипса, центр симметрии -- центром эллипса, отрезок между двумя вершинами, содержащий фокусы, называется большой осью эллипса, половина его длины -- большой полуосью эллипса. Отрезок между вершинами на оси симметрии, не содержащей фокусов, называется малой осью эллипса, половина его длины -- малой полуосью. Величина 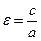 называется эксцентриситетом эллипса.
называется эксцентриситетом эллипса. 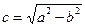 . Прямые, между которыми вытянут эллипс, называются директрисами, уравнения которых
. Прямые, между которыми вытянут эллипс, называются директрисами, уравнения которых  .
.
Если эллипс задан каноническим уравнением  , то его вершины имеют координаты (-а,0), (а,0), (0,b), (0,-b), большая полуось равна
, то его вершины имеют координаты (-а,0), (а,0), (0,b), (0,-b), большая полуось равна  , малая полуось равна
, малая полуось равна  . Величина
. Величина  , являющаяся половиной расстояния между фокусами, определяется из формулы
, являющаяся половиной расстояния между фокусами, определяется из формулы 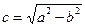 . Эксцентриситет
. Эксцентриситет  эллипса характеризует степень вытянутости эллипса. Чем ближе экcцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса
эллипса характеризует степень вытянутости эллипса. Чем ближе экcцентриситет к нулю, тем больше эллипс похож на окружность. Чем ближе эксцентриситет к 1, тем сильнее вытянут эллипс. Отметим, что по определению для эллипса  .
.
Замечание 1. Уравнение (2) было получено в предположении, что F 1 и F 2 и -- различные точки, то есть c > 0. Тогда b < a. Но кривую, определяемую уравнением, мы можем рассмотреть и в случае  , (c = 0). Уравнение в этом случае после умножения на
, (c = 0). Уравнение в этом случае после умножения на 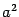 примет вид
примет вид  . Это -- уравнение окружности радиуса
. Это -- уравнение окружности радиуса  с центром в начале координат. Таким образом, можно рассматривать окружность как предельный вариант эллипса, когда
с центром в начале координат. Таким образом, можно рассматривать окружность как предельный вариант эллипса, когда  ,
,  , или, как иногда говорят математики, окружность является "вырожденным" эллипсом, у которого фокусы совпали.
, или, как иногда говорят математики, окружность является "вырожденным" эллипсом, у которого фокусы совпали.
Замечание 2. Если 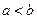 , то фокусы лежат на оси (Оу) и имеют координаты F 1(0,- с), F 2(0, с), где
, то фокусы лежат на оси (Оу) и имеют координаты F 1(0,- с), F 2(0, с), где  . Эксцентриситет
. Эксцентриситет  . Уравнения директрис
. Уравнения директрис 
Эллипс обладает многими замечательными свойствами. Приведем без доказательства одно из них.
Свойство эллипса. Пусть F 1, F 2 – фокусы эллипса, 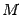 -- произвольная точка на эллипсе. Тогда нормаль (перпендукуляр к касательной) к эллипсу в точке
-- произвольная точка на эллипсе. Тогда нормаль (перпендукуляр к касательной) к эллипсу в точке 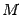 делит угол F 1 М F 2 пополам.
делит угол F 1 М F 2 пополам. 
Отражение лучей света от эллипса
Данное свойство имеет достаточно простой физический смысл. Если из одного фокуса выходит в плоскости эллипса луч света, то отразившись от самого эллипса, он обязательно пройдет через другой фокус. Возьмем поверхность, образованную вращением эллипса вокруг большой оси, и будем считать, что внутри она зеркальная. В один из фокусов поместим источник света. Тогда все лучи, выходящие из источника, отражаясь от поверхности, пройдут через другой фокус, то есть освещенность в обоих фокусах будет одинаковой.
 Замечание 3. Если центр эллипса лежит в точке М 0(х 0, у 0), то каноническое уравнение эллипса примет вид:
Замечание 3. Если центр эллипса лежит в точке М 0(х 0, у 0), то каноническое уравнение эллипса примет вид:  .
.
Пример 1. Постройте кривую  . Найдите фокусы и эксцентриситет.
. Найдите фокусы и эксцентриситет.
Решение. Разделим обе части уравнения на 36. Получаем уравнение  . Это -- каноническое уравнение эллипса,
. Это -- каноническое уравнение эллипса,  ,
,  .
.
Из соотношения находим  , фокусы F 1(
, фокусы F 1(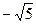 , 0), F 2(
, 0), F 2( , 0), эксцентриситет
, 0), эксцентриситет  .
.
Пример 2. Найдите фокусы и эксцентриситет эллипса  .
.
Решение. Уравнение запишем в виде  , где
, где  ,
,  , b > a. Отсюда
, b > a. Отсюда 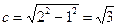 . Значит, фокусы имеют координаты F 1(
. Значит, фокусы имеют координаты F 1(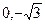 ), F 2(
), F 2(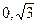 ). Эксцентриситет равен
). Эксцентриситет равен 
Дата добавления: 2015-07-11; просмотров: 76 | Нарушение авторских прав