Окружность. Кривые второго порядка

Кривые второго порядка

Определение 1.1 Окружностью называется геометрическое место точек, равноудалённых от одной и той же точки называемой центром.

Уравнение окружности имеет вид:

(1.1)

где точка С(x₀; y₀) – есть центр окружности, r – радиус окружности.

Если же центр окружности находится в начале координат, то её уравнение имеет вид:

(1.2)

Пример 1. Написать уравнение окружности с центром в точке и 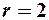и построить её.

Решение:

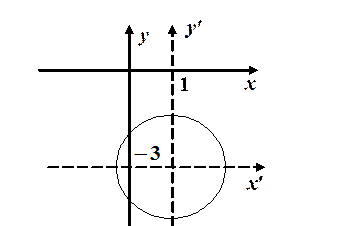
Эллипс

Определение 2.1 Эллипсом называется геометрическое место точек, сумма расстояний каждой из которых от двух данных точек 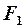и (фокусов) есть постоянная величина , большая , то есть

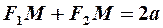и

Каноническое уравнение эллипса

(2.1)

при этом , 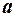– большая полуось эллипса; – малая полуось эллипса

Исследование эллипса

1. Эллипс целиком расположен в основном прямоугольнике, ограниченном прямыми:

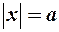
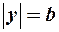
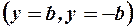
2. Точки пересечения с осями координат.

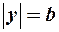имеем на оси ;

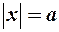имеем на оси .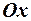

Точки - называются вершинами эллипса.

3. Эллипс симметричен относительно своих осей и центра.

4. Фокусы эллипса.

Точки и , где – являются фокусами эллипса.

– фокусное расстояние.

5. Эксцентриситет эллипса.

Определение 2.2 Число 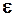, равное отношению полуфокусного расстояния к большой полуоси, называется эксцентриситетом эллипса.

, если

, если

Построение эллипса

1. Отмечаем на оси 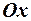точки и , а на оси точки и – вершины эллипса.

2. Проводим прямые – образуется основной прямоугольник.

3. Внутри основного прямоугольника строим гладкую кривую.

Если начало координат перенесено в точку – то получим уравнение эллипса со смещённым центром

(2.2)

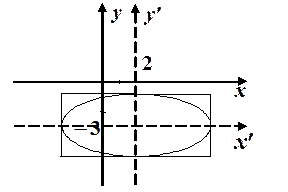
Задача. Построить эллипс

Дата добавления: 2015-07-11