Читайте также:
|
1. Эллипс не проходит через начало системы координат, так как координаты точки О(0,0) не удовлетворяют уравнению (3).
2. Найдем точки пересечения эллипса с осями координат. Для нахождения точки пересечения с осью О х полагаем в уравнении (3) у = 0 и находим x = ± a. Таким образом эллипс пересекает ось О х в точках A 1(- a, 0), A 2(a, 0). Аналогично находим, что эллипс пересекает ось О y в точках B 1(0,- b), B 2(0, b).
Точки A 1, A 2, B 1, B 2 называются вершинами эллипса, отрезки A 1 A 2, B 1 B 2 осями эллипса; | A 1 A 2| =2 a, | B 1 B 2| =2 b; числа a, b называются полуосями эллипса. Так как a > b, то A 1 A 2 называется большой осью, B 1 B 2 - малой осью.
3. Так как все переменные входят в уравнение (3) в четной степени, то вместе с точкой (x, y) эллипсу принадлежат четыре точки (± x, ± y) (с произвольными комбинациями знаков). Таким образом, эллипс симметричен относительно, всех координатных осей O x, O y и начала координат. Точка О называется центром эллипса.
4. Из уравнения эллипса находим, 
. Отсюда следует, что эллипс ограниченная линия, которая находится в прямоугольнике: - a £ x £ a, - b £ y £ b (см. рис. 1).
5. Исследуем поведение эллипса в первой четверти. Для этого выразим y из уравнения (3) через x:
.
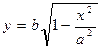Отсюда видим, в первой четверти на отрезке [0, a ] эллипс является графиком убывающей функции.
6. Любая прямая, проходящая через начало координат, пересекает эллипс в двух точках. Действительно, вертикальная прямая, ось O y, пересекает эллипс в двух вершинах, любую другую прямую можно задать уравнением y = kx, k Î R.
Дата добавления: 2015-07-11; просмотров: 165 | Нарушение авторских прав